
期权定价数值方法.ppt

是你****馨呀








亲,该文档总共41页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

期权定价数值方法.ppt
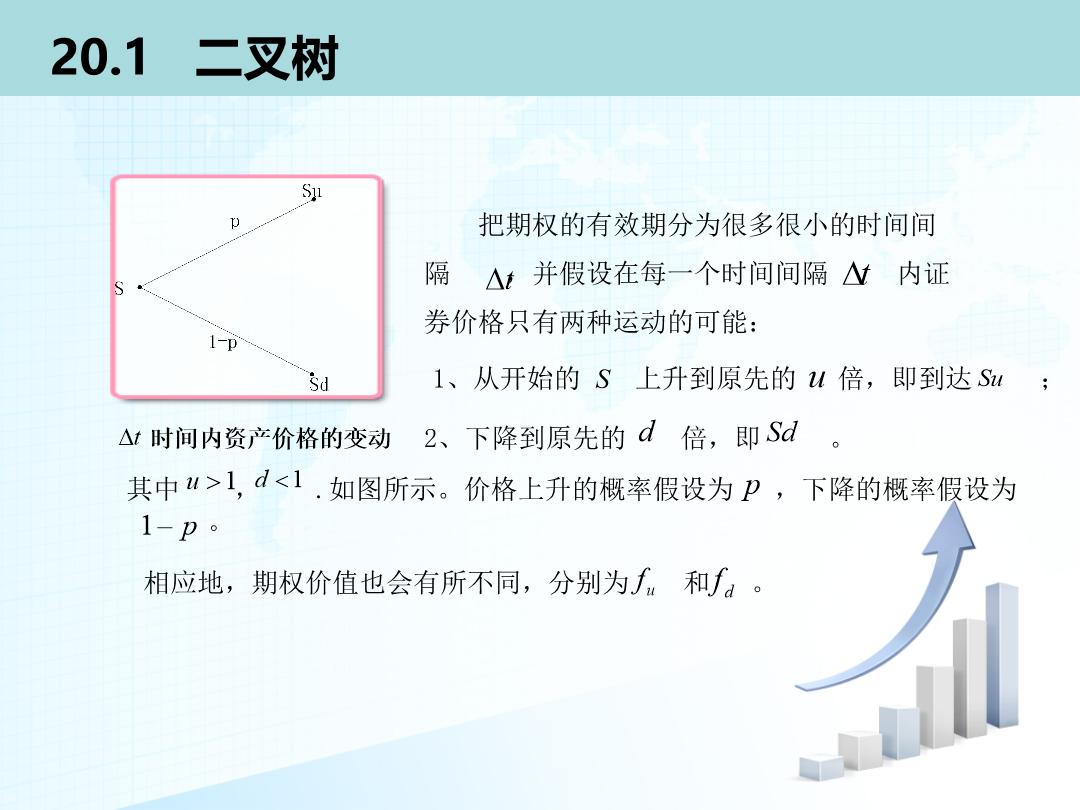
第20章基本数值方法20.1二叉树20.2采用二叉树对股指、货币与期货期权定价20.3对于支付股息股票的二叉树模型20.4构造树形的其他方法20.5参数依赖于时间的情形20.6蒙特卡罗模拟法20.7方差缩减程序20.8有限差分法1、从开始的上升到原先的倍即到达;构造投资组合包括份股票多头和1份看涨期权空头当。则组合为无风险组合在对衍生产品定价时可以假定世界是风险中性的。在风险中性世界里:(1)所有可交易证券

期权定价数值方法.ppt
第20章基本数值方法20.1二叉树20.2采用二叉树对股指、货币与期货期权定价20.3对于支付股息股票的二叉树模型20.4构造树形的其他方法20.5参数依赖于时间的情形20.6蒙特卡罗模拟法20.7方差缩减程序20.8有限差分法1、从开始的上升到原先的倍即到达;构造投资组合包括份股票多头和1份看涨期权空头当。则组合为无风险组合在对衍生产品定价时可以假定世界是风险中性的。在风险中性世界里:(1)所有可交易证券

期权定价的数值方法wxp.pptx
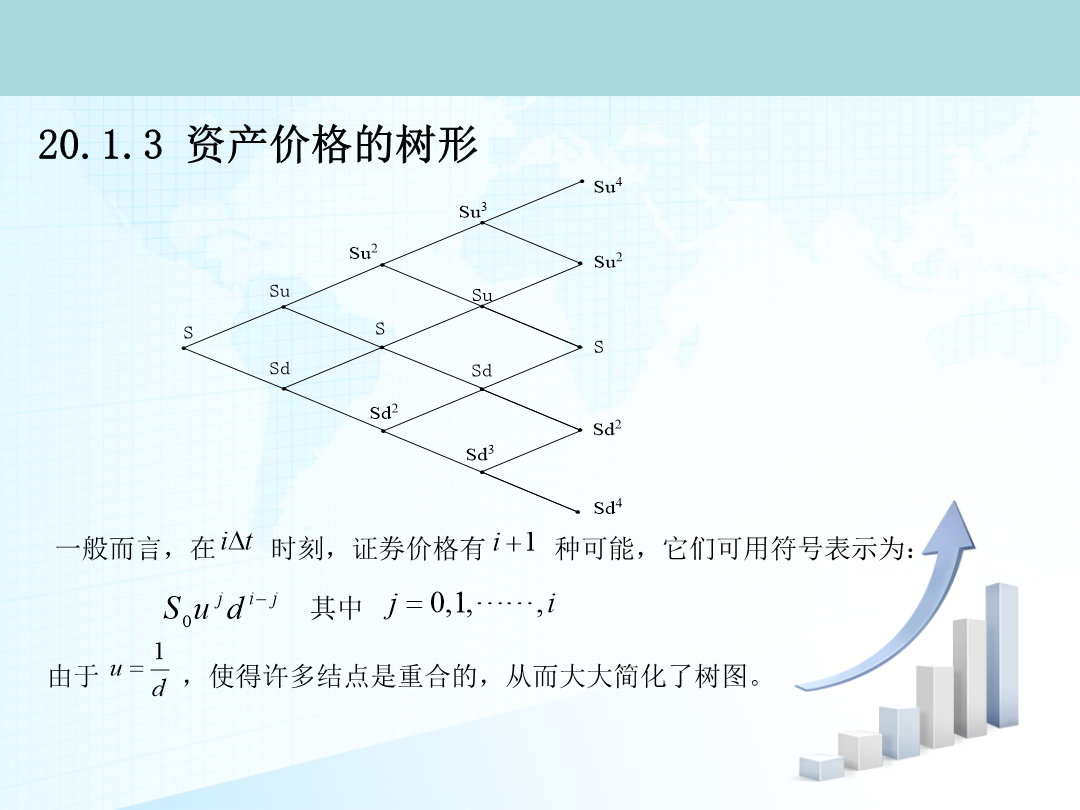
第八章期权定价旳数值措施第一节二叉树期权定价模型第二节蒙特卡罗模拟第三节有限差分措施二叉树模型旳思想实际上是在用大量离散旳小幅度二值运动来模拟连续旳资产价格运动无套利定价法:构造投资组合涉及份股票多头和1份看涨期权空头当时,股票价格旳变动对组合无影响则组合为无风险组合证券价格旳树型构造应用多步二叉树模型来表达证券价格变化旳完整树形构造如图:证券价格旳树型构造(三)倒推定价法举例阐明续美式看跌期权二叉树二叉树措施旳一般定价过程支付连续红利率资产旳期权定价支付已知红利率资产旳期权定价已知红利额已知红利额利率是

期权定价问题的数值方法.pdf
系统科学与数学乞对。么,,一期权定价问题的数值方法刘棠天津财经学院基础部,天津南开大学天津大学刘徽应用数学中心,天津张盘铭天津财经学院科研处,天津摘要本文研究以股票为标的资产的美式看跌期权定价问题的数值方法,即有限元方法通过将所考虑的问题转化为等价的变分不等式,并利用积分恒等式与超逼近分析技术,得到了半离散有限元方法的最优一模与一模的误差估计关键词美式看跌期权,变分不等式,有限元方法,最优误差估计主题分类号,,,引言早在世纪欧洲和美国就己经有了简单的期权交易,到了世纪年代,期权交易在投资者中开始普及特别是

期权定价问题的数值方法.pdf
系统科学与数学乞对。么,,一期权定价问题的数值方法刘棠天津财经学院基础部,天津南开大学天津大学刘徽应用数学中心,天津张盘铭天津财经学院科研处,天津摘要本文研究以股票为标的资产的美式看跌期权定价问题的数值方法,即有限元方法通过将所考虑的问题转化为等价的变分不等式,并利用积分恒等式与超逼近分析技术,得到了半离散有限元方法的最优一模与一模的误差估计关键词美式看跌期权,变分不等式,有限元方法,最优误差估计主题分类号,,,引言早在世纪欧洲和美国就己经有了简单的期权交易,到了世纪年代,期权交易在投资者中开始普及特别是
