预览加载中，请您耐心等待几秒...

从特殊三棱锥到一般三棱锥问题.ppt

预览
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10

亲，该文档总共26页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示 文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

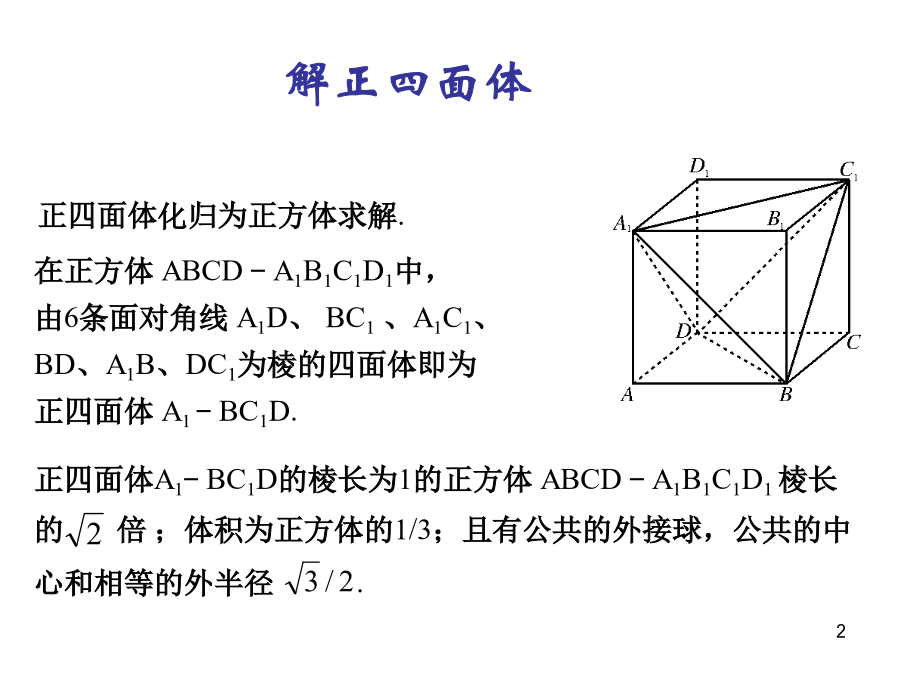
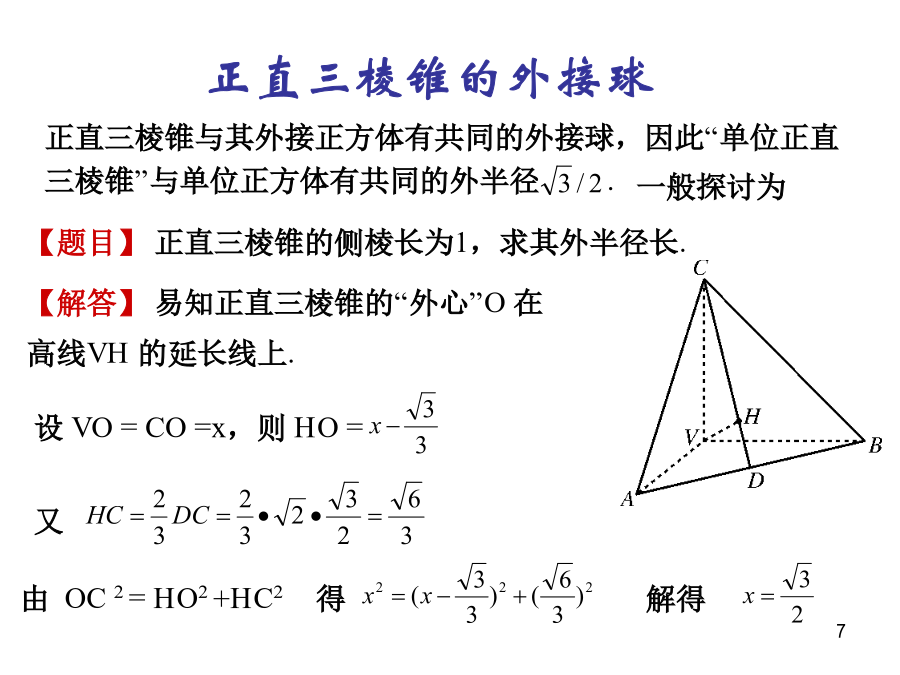
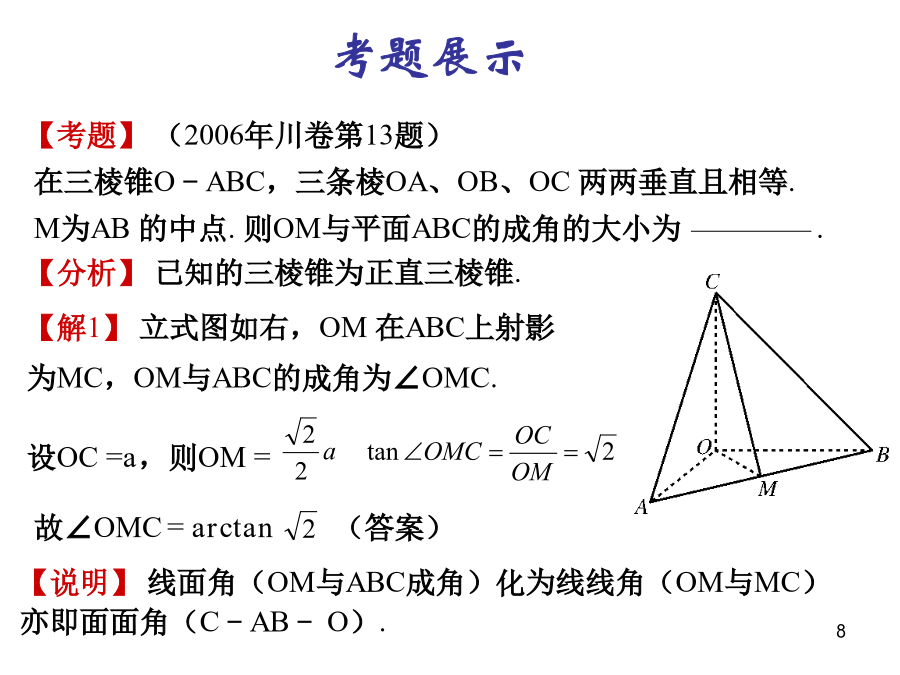
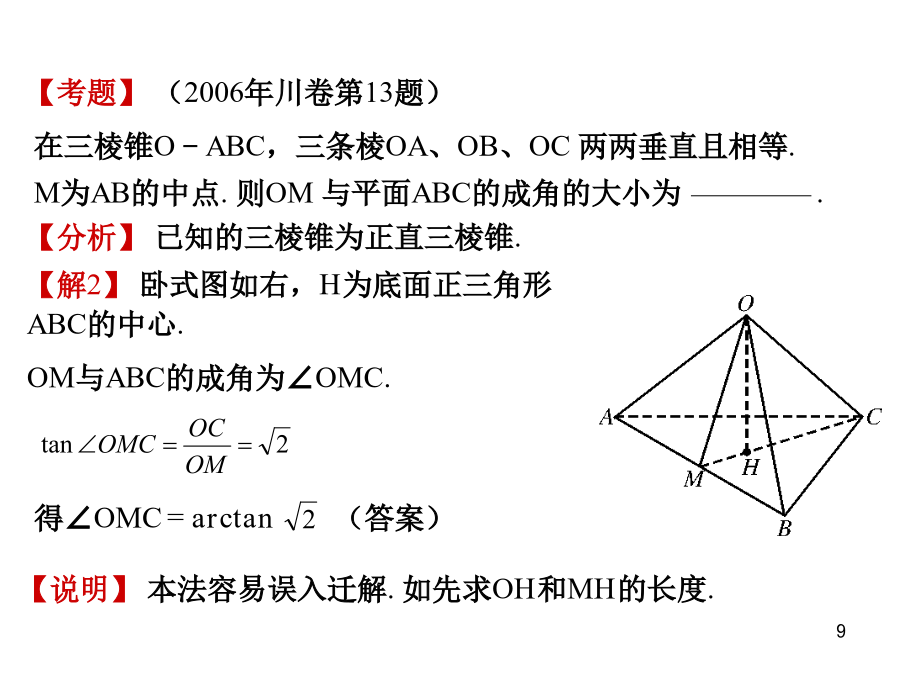
解三棱锥解正四面体“正直”三棱锥解正直三棱锥正直三棱锥的高线【题目】若正直三棱锥V-ABC的侧棱长为VA=1.求它高线VH的长度.正直三棱锥的外接球考题展示【考题】（2006年川卷第13题）正方体内接三棱锥的个数“长棱”三棱锥直正三棱锥解直正三角形【题目】三棱锥P—ABC中，PA⊥面ABC，且PA=，正三棱锥正三棱锥的判断正三棱锥的判断正三棱锥的判断正三棱锥的判断【证明（）】 ∠ACB=90°，∴BC⊥AC. ∵PA⊥底面ABCD，∴PA⊥BC ∴BC⊥平面PAC.【题目】四棱锥P–ABCD中，AB∥CD, AD=CD=1，∠BAD=120°，PA=,ACB=90°.【题目】四棱锥P–ABCD中，AB∥CD, AD=CD=1，∠BAD=120°，PA=,∠ACB=90°.三棱锥的外心外心位置的确定（1）试确定三棱锥外心位置.在“长棱”上猜外心