
克里金插值(kriging).ppt

玄静****写意







亲,该文档总共107页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

克里金插值(kriging).ppt
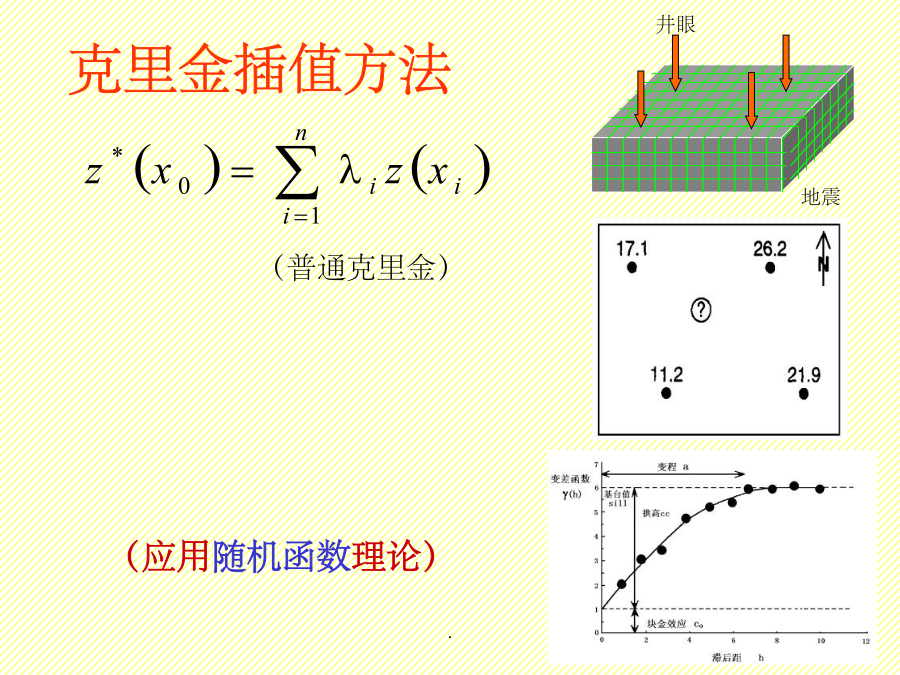
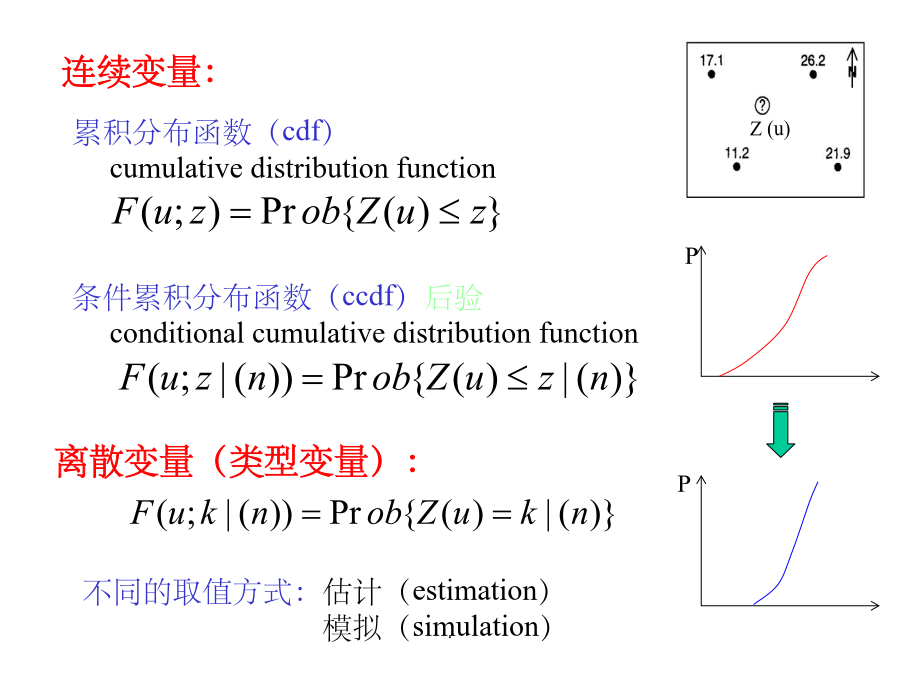
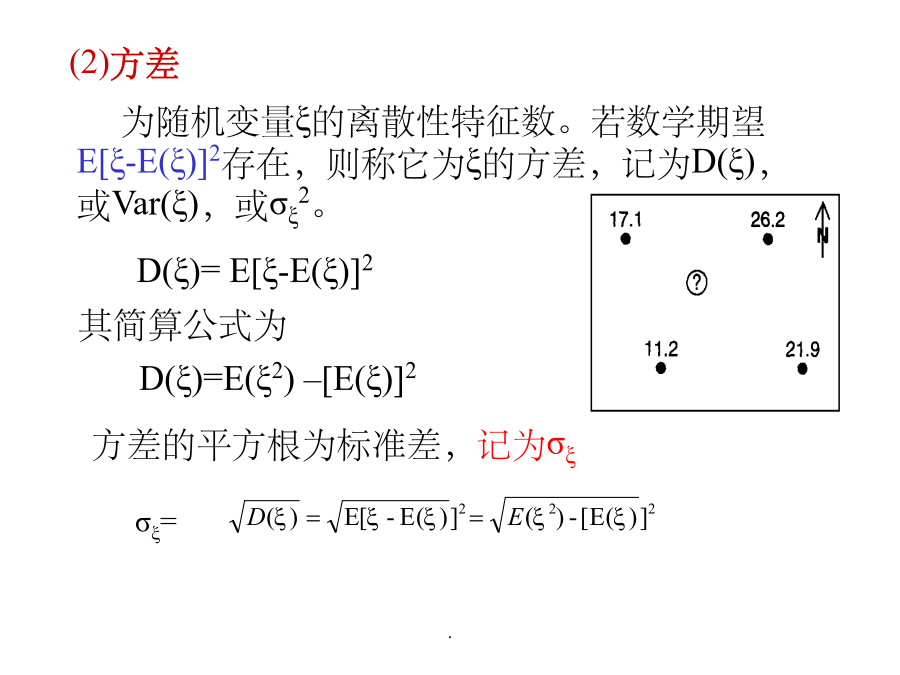
地质统计学H.S.Sichel(1947)克里金插值方法连续变量:①设离散型随机变量ξ的所有可能取值为x1,x2,…,其相应的概率为②设连续型随机变量ξ的可能取值区间为(-∞,+∞),p(x)为其概率密度函数,若无穷积分绝对收敛,则称它为ξ的数学期望,记为E(ξ)。为随机变量ξ的离散性特征数。若数学期望E[ξ-E(ξ)]2存在,则称它为ξ的方差,记为D(ξ),或Var(ξ),或σξ2。研究范围内的一组随机变量。二个随机变量ξ,η的协方差为二维随机变量(ξ,η)的二阶混合中心矩μ11,记为Cov(ξ,η),

克里金插值(kriging).ppt
地质统计学H.S.Sichel(1947)克里金插值方法连续变量:①设离散型随机变量ξ的所有可能取值为x1,x2,…,其相应的概率为②设连续型随机变量ξ的可能取值区间为(-∞,+∞),p(x)为其概率密度函数,若无穷积分绝对收敛,则称它为ξ的数学期望,记为E(ξ)。为随机变量ξ的离散性特征数。若数学期望E[ξ-E(ξ)]2存在,则称它为ξ的方差,记为D(ξ),或Var(ξ),或σξ2。研究范围内的一组随机变量。二个随机变量ξ,η的协方差为二维随机变量(ξ,η)的二阶混合中心矩μ11,记为Cov(ξ,η),

kriging克里金方法克里金插值.pptx
会计学地质(dìzhì)统计学H.S.Sichel(1947)克里金插值方法(fāngfǎ)连续变量:①设离散型随机变量ξ的所有可能取值为x1,x2,…,其相应(xiāngyīng)的概率为②设连续型随机变量ξ的可能取值区间(qūjiān)为(-∞,+∞),p(x)为其概率密度函数,若无穷积分绝对收敛,则称它为ξ的数学期望,记为E(ξ)。为随机变量ξ的离散性特征数。若数学期望E[ξ-E(ξ)]2存在(cúnzài),则称它为ξ的方差,记为D(ξ),或Var(ξ),或σξ2。研究(yánjiū)范围内的一组

《克里金插值》.ppt
精选课件精选课件精选课件精选课件精选课件精选课件精选课件精选课件精选课件精选课件精选课件精选课件精选课件

克里金插值法.docx
克里金插值法克里金插值法又称空间局部插值法,是以变异函数理论和结构分析为基础,在有限区域内对区域化变量进行无偏最优估计的一种方法,是地统计学的主要内容之一,由南非矿产工程师D.Matheron于1951年在寻找金矿时首次提出,法国著名统计学家G.Matheron随后将该方法理论化、系统化,并命名为Kriging,即克里金插值法。1克里金插值法原理克里金插值法的适用范围为区域化变量存在空间相关性,即如果变异函数和结构分析的结果表明区域化变量存在空间相关性,则可以利用克里金插值法进行内插或外推。其实质是利用区
