
静态线性系统最优化模型及求解方法【共25张PPT】.ppt

盼易****君a






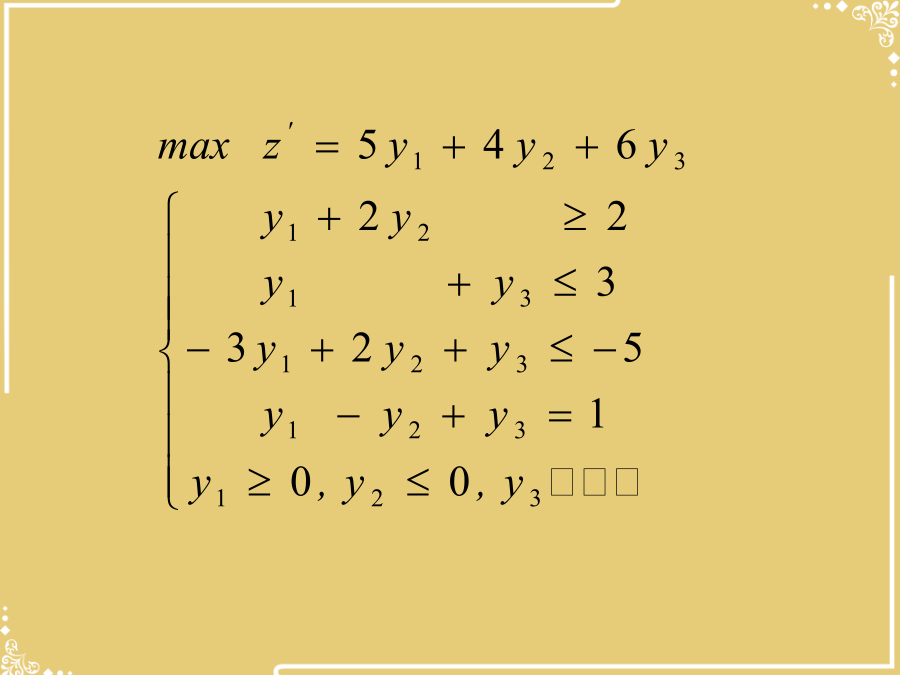

亲,该文档总共25页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

静态线性系统最优化模型及求解方法【共25张PPT】.ppt
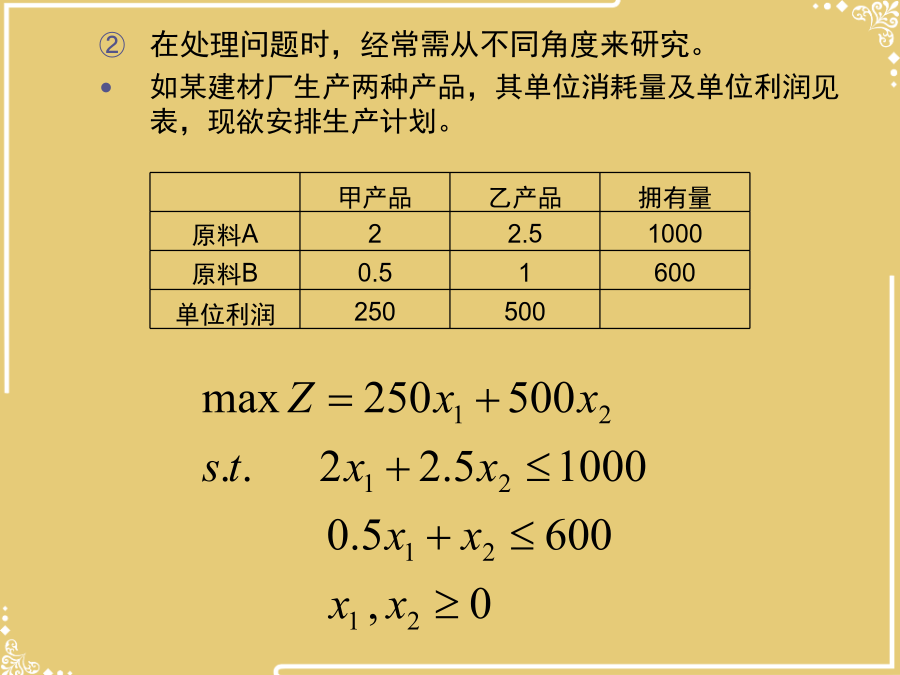
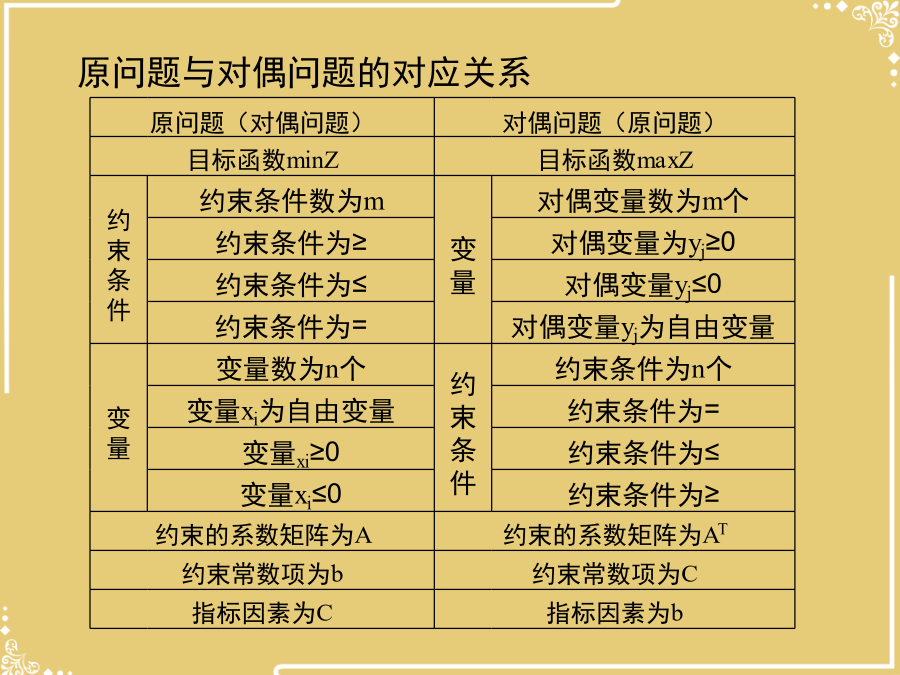
第六章静态线性系统最优化模型及求解方法优选第六章静态线性系统最优化模型及求解方法在处理问题时,经常需从不同角度来研究。如某建材厂生产两种产品,其单位消耗量及单位利润见表,现欲安排生产计划。如果从另一个角度研究,现将原料出售,又不低于产品生产所获得的利润,两种原料出售的最低利润(在成本的基础上的加价)应为多少合算?线性规划的对偶理论原问题与对偶问题的对应关系求下述线性规划原问题的对偶问题区分有些资源的增减并不影响目标值,这类资源是长线资源,某些资源的增减对目标值影响很大,这种资源是较稀缺的资源,称为短线资源

静态线性系统最优化模型及求解方法【共25张】.ppt
第六章静态线性系统最优化模型及求解方法优选第六章静态线性系统最优化模型及求解方法在处理问题时,经常需从不同角度来研究。如某建材厂生产两种产品,其单位消耗量及单位利润见表,现欲安排生产计划。如果从另一个角度研究,现将原料出售,又不低于产品生产所获得的利润,两种原料出售的最低利润(在成本的基础上的加价)应为多少合算?线性规划的对偶理论原问题与对偶问题的对应关系求下述线性规划原问题的对偶问题区分有些资源的增减并不影响目标值,这类资源是长线资源,某些资源的增减对目标值影响很大,这种资源是较稀缺的资源,称为短线资源

静态优化模型PPT课件.ppt
第三章简单的优化模型现实世界中普遍存在着优化问题.3.1存贮模型问题分析与思考这是一个优化问题,关键在建立目标函数.模型假设模型建立模型求解经济批量订货公式(EOQ公式)允许缺货的存贮模型每天总费用平均值(目标函数)不允许缺货模型允许缺货模型存贮模型3.2生猪的出售时机求t使Q(t)最大敏感性分析敏感性分析强健性分析3.3森林救火关键是对B(t)作出合理的简化假设.模型假设模型建立模型建立模型应用3.4消费者的选择当消费者购得数量分别为x1,x2的甲乙两种商品时,得到的效用可用函数u(x1,x2)度量,称

静态优化模型.ppt
第三章简单的优化模型现实世界中普遍存在着优化问题.3.1存贮模型问题分析与思考这是一个优化问题,关键在建立目标函数.模型假设模型建立模型求解经济批量订货公式(EOQ公式)允许缺货的存贮模型每天总费用平均值(目标函数)不允许缺货模型允许缺货模型存贮模型3.2生猪的出售时机求t使Q(t)最大敏感性分析敏感性分析强健性分析3.3森林救火关键是对B(t)作出合理的简化假设.模型假设模型建立模型建立模型应用3.4消费者的选择当消费者购得数量分别为x1,x2的甲乙两种商品时,得到的效用可用函数u(x1,x2)度量,称

优化模型及求解.ppt
优化模型及求解在工程技术、经济管理、科学研究和日常生活中,我们经常会遇到的一类决策问题是:在一系列客观或主观条件限制下,寻求使所关注的某个或多个指标达到最优的决策。这类问题称为最优化问题,研究处理这类问题的数学方法称为最优化方法,它也是运筹学和管理科学中解决定量问题的基本方法。在决策科学化、定量化的呼声日益高涨的今天,用最优化方法来解决定量的决策问题无疑是符合时代潮流与要求的,也应该是当今大学生必备的知识之一。通常人们解决优化问题的手段大致有以下几种:(1)依赖过去的经验判断面临的问题。这种方法似乎切实可
