优化模型及求解.ppt

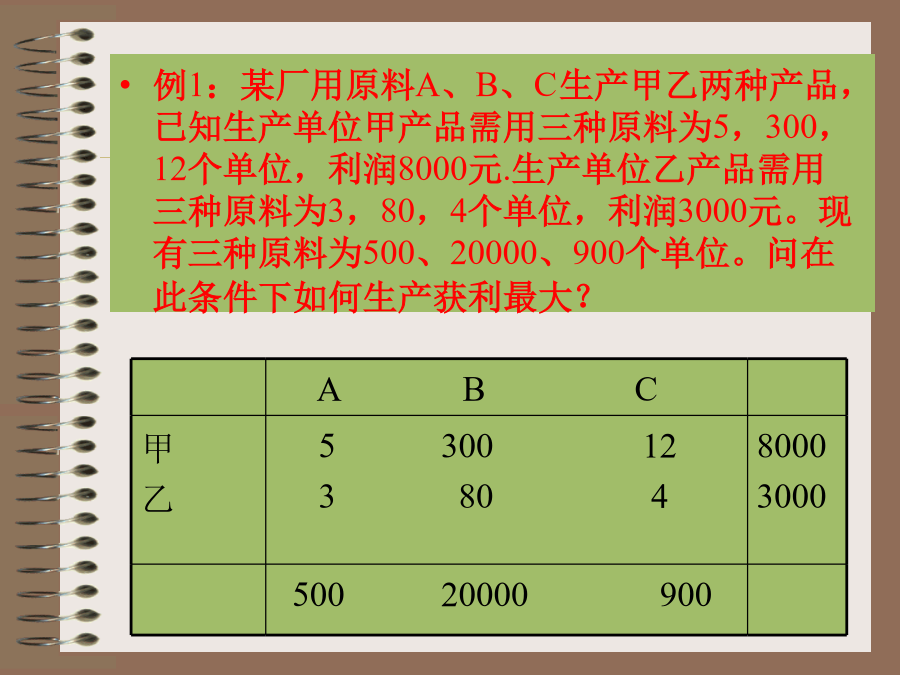
优化模型及求解在工程技术、经济管理、科学研究和日常生活中，我们经常会遇到的一类决策问题是：在一系列客观或主观条件限制下，寻求使所关注的某个或多个指标达到最优的决策。这类问题称为最优化问题，研究处理这类问题的数学方法称为最优化方法，它也是运筹学和管理科学中解决定量问题的基本方法。在决策科学化、定量化的呼声日益高涨的今天，用最优化方法来解决定量的决策问题无疑是符合时代潮流与要求的，也应该是当今大学生必备的知识之一。通常人们解决优化问题的手段大致有以下几种：
（1）依赖过去的经验判断面临的问题。这种方法似乎切实可行，但是在处理过程中会融入决策者大量的主观因素，结果未必是好的，且存在较大的风险。
（2）大量做试验进行比较。这虽然人为因素减少，比较真实可靠，但是投入费用大且结果未必是最好的。
（3）用数学方法建立优化模型求得最优决策，称为优化建模方法，所得模型称为优化模型。用最优化方法解决决策问题包括两个基本步骤：首先，我们需要把实际决策问题翻译、表述成数学最优化的形式，即用数学建模方法建立决策问题的优化模型，简称为优化建模；其次，建立优化模型后，我们需要选择、利用优化方法和工具求解模型。优化建模方法自然具有一般的数学建模方法的共同特性，但优化模型又是一类既重要、又特殊的数学模型，因此优化建模方法又具有一定的特殊性和专业性。此外，由于优化模型的种类很多，很多模型目前还没有有效的求解方法，不同的算法用于求解不同模型的效果可能差异很大，如何利用优化软件求解优化模型也有一定的专业性和技巧性。优化模型是一种特殊的数学模型，优化建模方法是一种特殊的数学建模方法，优化模型一般由以下三个要素构成。例1：某厂用原料A、B、C生产甲乙两种产品，已知生产单位甲产品需用三种原料为5，300，12个单位，利润8000元.生产单位乙产品需用三种原料为3，80，4个单位，利润3000元。现有三种原料为500、20000、900个单位。问在此条件下如何生产获利最大？这是一个简单的二元线性规划问题，数学
模型为：例2：某服务部门一周中每天需要不同数目的雇员：周一到周四每天至少需要50人，周五至少需要80人，周六和周日至少需要90人。规定应聘者需连续工作5天，试确定聘用方案，即周一到周日每天聘用多少人，可在满足需要的条件下聘用总人数最少。数学模型为：例3：准备从5名游泳运动员中选择4人参加4×100m混合泳接力赛。5名队员4种泳姿的百米成绩见下表，问应如何选拔队员？引入0-1变量xij表示队员i参加泳姿j的比赛，则有总用时为253.2秒例4：某公司需要决定一年中四个季度的生
产量，已知每个季度的产品需求量分别是
40，60，25，75个单位，需求必须按时满
足。每个季度的正常常生产能力是40个单
位，单位产品的生产费用为400，若加班生
产，单位产品的生产费用为450，每个季度
末，单位产品的库存费用为20，假定生产
提前期为0，初始库存为10，如何安排生产
可使总费用最少？我们用x,z,j,k分别表示需求量、正常生产量、加班生产量和库存量，则有下面的数学模型：一般来说，LINGO中建立的优化模型由以下三部分组成LINGO的运算符和函数基本的数学函数
@abs(x)、@exp(x)、@log(x)、@sin(x)、@cos(x)、@tan(x)、@mod(x,y)、@floor(x)、@sign(x)、@smax(list)、@smin(list)@function(setname[(set_index_list)[|condition]]:expression_list);其中
function是集合函数名，是for，max,min,prod,sum五种之一@for(集合元素的循环函数)：对集合setname的每个元素独立的生成表达式，表达式由expression_list描述（通常是优化问题的描述）集合操作函数
集合操作函数是指对集合进行操作的函数，主要有@IN,@INDEX,@WRAP,@SIZE四种错误码错误码例5：某公司用两种原油A与B加工甲乙
两种标号的汽油，甲乙两种汽油含原油
A的最低比例分别为50%和60%，每吨
售价分别为4.8千元和5.6千元。公司现有
原油A和B分别为500t和1000t，还可以
在市场上买到不超过1500t的原油A，其
市场价为购买量不超过500t时单价为每
吨10千元，超过500不到1000吨时，超
过部分每吨8千元，若购买超过1000吨，
超过部分每吨6千元。该公司应该如何
安排生产？问题分析设原油A用于生产甲乙两种汽油的数量分别为x11和x12
原油B用于生产甲乙两种汽油的数量分别为x21和x22，
则目标函数为总利润函数最大：模型求解第二种解法：引入0-1变量将第一种解法中的非线性约束转化为线性约束。第三种解法：直接处理分