
递推最小二乘辨识教育课件.ppt

一只****写意







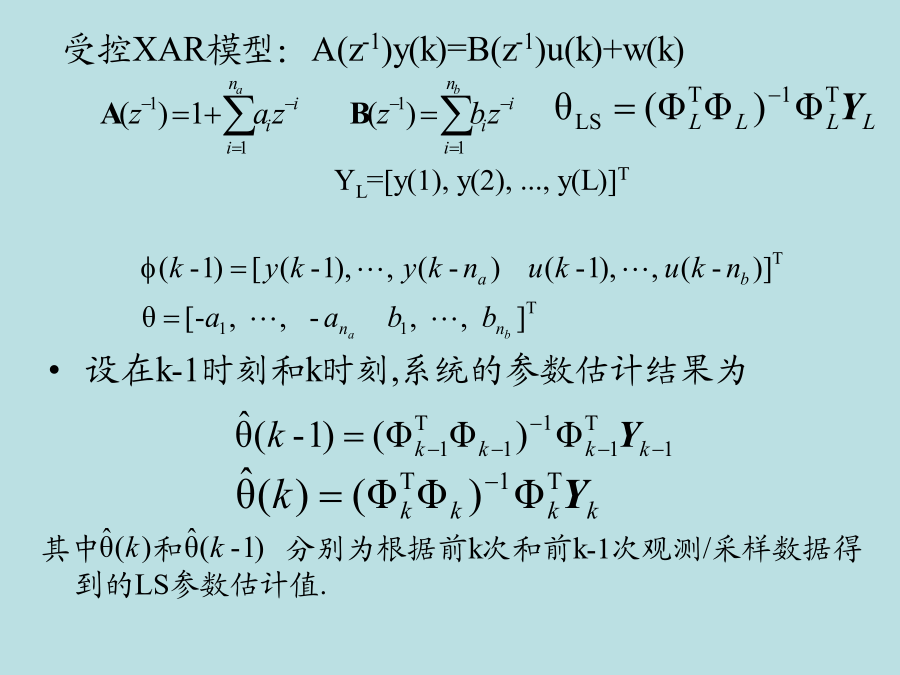


亲,该文档总共33页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

递推最小二乘辨识教育课件.ppt
递推最小二乘辨识PPT讲座时变参数辨识故障监测与诊断仿真等.递推辨识算法的思想可以概括成新的参数估计值=旧的参数估计值+修正项即新的递推参数估计值是在旧的递推估计值的基础上修正而成,这就是递推的概念.递推算法不仅可减少计算量和存储量,而且能实现在线实时辨识.递推算法的特性本讲主要讲授递推最小二乘(RecursiveLeast-square,RLS)法的思想及推导过程,主要内容为:递推算法加权RLS法和渐消记忆RLS法1递推算法递推算法就是依时间顺序,每获得一次新的观测数据就修正一次参数估计值,随着时间的推

递推最小二乘辨识.docx
实验4递推最小二乘法的实现实验报告哈尔滨工业大学航天学院控制科学与工程系专业:自动化班级:1040101姓名:日期:2013年10月23日1.实验题目:递推最小二乘法的实现2.实验目的:熟悉并掌握递推最小二乘法的算法原理。3.实验主要原理给定系统(1)其中,为待辨识的未知参数,是不相关随机序列。为系统的输出,为系统的输入。分别测出个输出、输入值,则可写出个方程,具体写成矩阵形式,有(2)设,则式(2)可写为(3)式中:y为N维输出向量;为N维噪声向量;为维参数向量;为测量矩阵。为了尽量减小噪声对估值的影响

递推最小二乘辨识.ppt
递推最小二乘法(RLS)上一节中已经给出了LS法的一次成批型算法,即在获得所有系统输入输出检测数据之后,利用LS估计式一次性计算出估计值.成批型LS法在具体使用时不仅计算量大,占用内存多,而且不能很好适用于在线辨识.随着控制科学和系统科学的发展,迫切需要发展一种递推参数估计算法,以能实现实时在线地进行辨识系统模型参数以供进行实时控制和预报,如在线估计自适应控制和预报时变参数辨识故障监测与诊断仿真等.递推辨识算法的思想可以概括成新的参数估计值=旧的参数估计值+修正项即新的递推参数估计值是在旧的递推估计值的基

递推最小二乘估计及模型阶次辨识.docx
《系统辨识基础》第19讲要点实验二递推最小二乘估计(RLS)及模型阶次辨识(F-Test)一、实验目的①通过实验,掌握递推最小二乘参数辨识方法②通过实验,掌握F-Test模型阶次辨识方法二、实验内容1、仿真模型实验所用的仿真模型如下:框图表示e(k)++v(k)u(k)z(k)y(k)模型表示其中u(k)和z(k)分别为模型的输入和输出变量;v(k)为零均值、方差为1、服从正态分布的白噪声;为噪声的标准差(实验时,可取0.0、0.1、0.5、1.0);输入变量u(k)采用M序列,其特征多项式取,幅度取1.

递推最小二乘估计及模型阶次辨识.doc
实验二递推最小二乘估计(RLS)及模型阶次辨识(F-Test)1实验方案设计1.1生成输入数据和噪声用M序列作为辨识的输入信号,噪声采用标准正态分布的白噪声。生成白噪声时,首先利用乘同余法生成U[0,1]均匀分布的随机数,再利用U[0,1]均匀分布的随机数生成标准正态分布的白噪声。1.2过程仿真辨识模型的形式取,为方便起见,取即用M序列作为辨识的输入信号。1.3递推遗忘因子法数据长度L取534,初值1.4计算损失函数、噪声标准差损失函数噪声标准差1.6F-Test定阶法计算模型阶次统计量其中,为相应阶次下
