
基于成形法加工工艺的螺旋锥齿轮齿顶曲线方程的求解.docx

快乐****蜜蜂



在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

基于成形法加工工艺的螺旋锥齿轮齿顶曲线方程的求解.docx
基于成形法加工工艺的螺旋锥齿轮齿顶曲线方程的求解螺旋锥齿轮是一种广泛应用于工业领域的机械传动元件,其齿顶曲线是其性能指标之一。因为螺旋锥齿轮是通过成形法加工制造的,在加工工艺的影响下,齿顶曲线的形状具有一定的变化。因此,本论文旨在研究螺旋锥齿轮齿顶曲线方程的求解问题,并探讨加工工艺对齿顶曲线的影响。一、螺旋锥齿轮齿顶曲线方程的求解1.1螺旋锥齿轮齿顶曲线螺旋锥齿轮的齿顶曲线是指齿面上最高点的曲线。螺旋锥齿轮齿顶曲线分为三段,即齿根段、齿顶段和齿峰段。在实际加工中,齿顶曲线通常用参数方程形式表示。假设齿顶曲
等高螺旋锥齿轮齿顶倒棱的加工方法.pdf
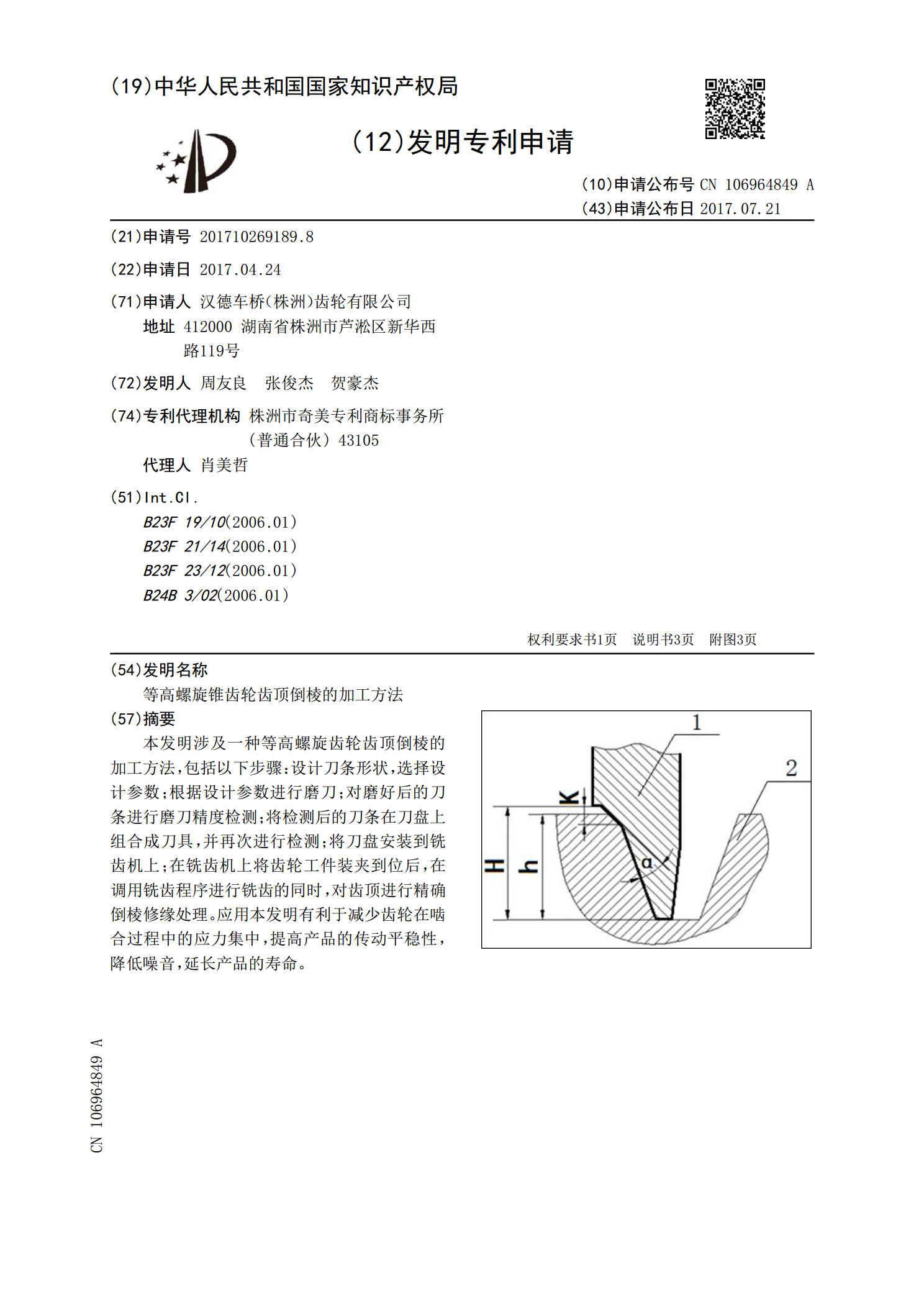
本发明涉及一种等高螺旋齿轮齿顶倒棱的加工方法,包括以下步骤:设计刀条形状,选择设计参数;根据设计参数进行磨刀;对磨好后的刀条进行磨刀精度检测;将检测后的刀条在刀盘上组合成刀具,并再次进行检测;将刀盘安装到铣齿机上;在铣齿机上将齿轮工件装夹到位后,在调用铣齿程序进行铣齿的同时,对齿顶进行精确倒棱修缘处理。应用本发明有利于减少齿轮在啮合过程中的应力集中,提高产品的传动平稳性,降低噪音,延长产品的寿命。

一种螺旋锥齿齿顶倒圆加工方法.pdf
本发明提供一种螺旋锥齿齿顶倒圆加工方法,包括:获取待倒圆的螺旋锥齿的数学模型;将所述待倒圆的螺旋锥齿的数学模型导入UnigraphicsNX软件,采用所述UnigraphicsNX软件的CAD模块,获取所述螺旋锥齿轮齿顶倒圆部分的数学模型;根据所述螺旋锥齿轮齿顶倒圆部分的数学模型和走刀加工方式,生成机床数控程序;采用所述机床数控程序对所述待倒圆的螺旋锥齿进行倒圆。

曲线齿锥齿轮的数控加工工艺研究.docx
曲线齿锥齿轮的数控加工工艺研究标题:曲线齿锥齿轮的数控加工工艺研究摘要:曲线齿锥齿轮是一种常用于传动系统中的齿轮副。本论文主要研究曲线齿锥齿轮的数控加工工艺,旨在提高加工精度和效率。本文分析了曲线齿锥齿轮的结构特点,探讨了数控加工的原理和方法,并结合实际案例探讨了数控加工工艺对曲线齿锥齿轮加工的影响。通过研究,我们发现采用数控加工工艺可以有效提高曲线齿锥齿轮加工的精度和效率,并提供了解决方案和建议。关键词:曲线齿锥齿轮、数控加工、加工精度、加工效率、工艺优化第一章引言1.1研究背景和意义1.2研究目的和内

一种等高齿螺旋锥齿轮齿面方程的简化方法.docx
一种等高齿螺旋锥齿轮齿面方程的简化方法等高齿螺旋锥齿轮是一种常用的齿轮传动形式,它的传动效率高、噪声小等优点被广泛应用于各种机械传动系统中。而在设计等高齿螺旋锥齿轮时,其齿面的准确描述是非常重要的,而简化齿面方程是一种有效且实用的方法,可以大大提高齿轮传动的设计效率。因此,本文以等高齿螺旋锥齿轮的齿面简化方法为研究方向,探讨其原理、方法及应用等内容。一、等高齿螺旋锥齿轮的齿面简化方法原理等高齿螺旋锥齿轮的齿面由于其结构特点,需要采用几何设计法进行描述。而几何设计法的主要思想是将齿轮齿面划分为若干个简单曲面
