
stata回归结果详解stata回归解释(与“回归”相关文档).pptx

赫赫****等你




亲,该文档总共27页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

stata回归结果详解stata回归解释(与“回归”相关文档).pptx
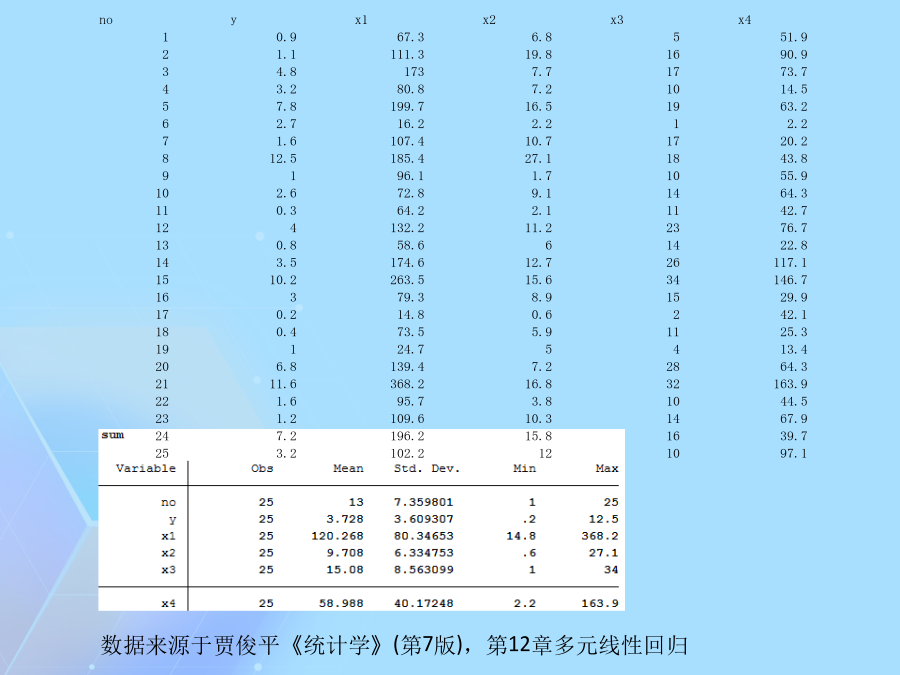
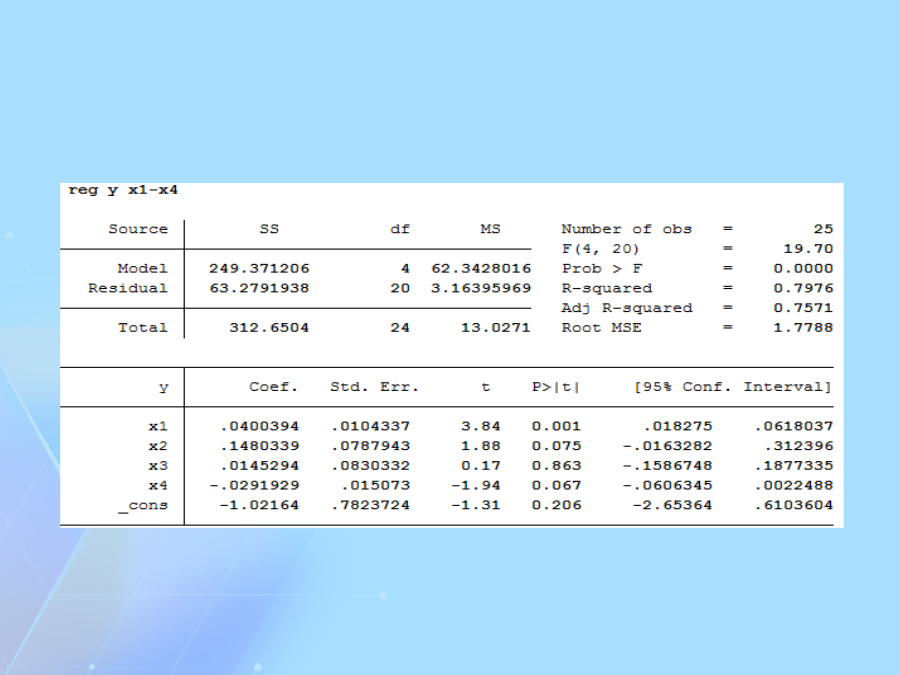
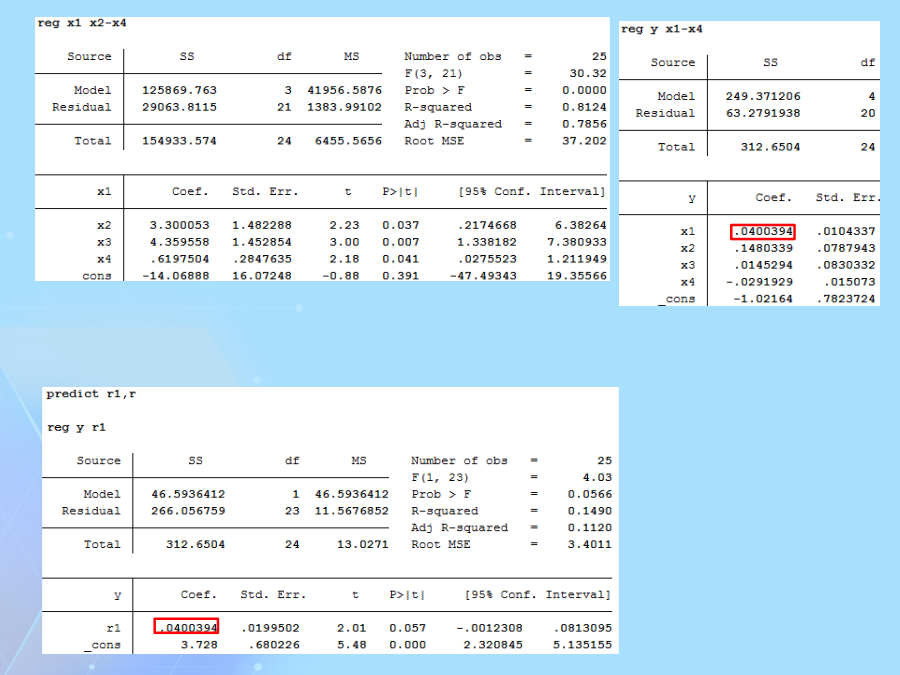
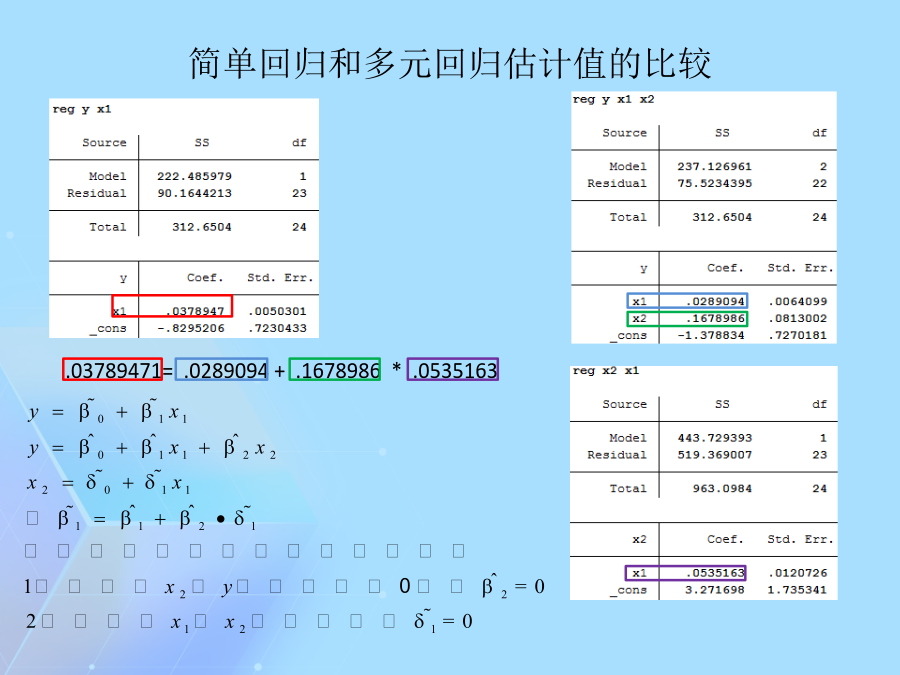
stata回归结果详解-stata回归解释数据来源于贾俊平《统计学》(第7版),第12章多元线性回归第二列SS对应的是误差平方和,或称变差。1.第一行为回归平方和或回归变差SSR,表示因变量的预测值对其平均值的总偏差。2.第二行为剩余平方和(也称残差平方和或剩余变差)SSE,是因变量对其预测值的总偏差,这个数值越大,拟合效果越差,y的标准误差即由SSE给出。3.第三行为总平方和或总变差SST,表示因变量对其平均值的总偏差。4.容易验证249.37+63.28=312.65回归系数对多元回归“排除其它变量影

stata回归结果详解.ppt
stata回归结果详解数据来源于贾俊平《统计学》(第7版),第12章多元线性回归第二列SS对应的是误差平方和,或称变差。1.第一行为回归平方和或回归变差SSR,表示因变量的预测值对其平均值的总偏差。2.第二行为剩余平方和(也称残差平方和或剩余变差)SSE,是因变量对其预测值的总偏差,这个数值越大,拟合效果越差,y的标准误差即由SSE给出。3.第三行为总平方和或总变差SST,表示因变量对其平均值的总偏差。4.容易验证249.37+63.28=312.65回归系数对多元回归“排除其它变量影响”的解释简单回归和

stata回归结果详解PPT课件.pptx
stata回归结果详解数据来源于贾俊平《统计学》(第7版),第12章多元线性回归3第二列SS对应的是误差平方和,或称变差。1.第一行为回归平方和或回归变差SSR,表示因变量的预测值对其平均值的总偏差。2.第二行为剩余平方和(也称残差平方和或剩余变差)SSE,是因变量对其预测值的总偏差,这个数值越大,拟合效果越差,y的标准误差即由SSE给出。3.第三行为总平方和或总变差SST,表示因变量对其平均值的总偏差。4.容易验证249.37+63.28=312.65回归系数对多元回归“排除其它变量影响”的解释简单回归

STATA 回归分析.docx
在此处利用两个简单的回归分析案例让初学者学会使用STATA进行回归分析。STATA版本:11.0案例1:某实验得到如下数据x12345y45.56.27.78.5对xy进行回归分析。第一步:输入数据(原始方法)1.在命令窗口输入inputxy/有空格2.回车得到:3.再输入:1425.536.247.758.5end4.输入list得到5.输入regyx得到回归结果回归结果:T=(15.15)(12.32)R2=0.98解释一下:SS是平方和,它所在列的三个数值分别为回归误差平方和(SSE)、残差平方和(

STATA与面板数据回归.ppt
面板数据模型与stata软件的应用一、面板数据类型表11996-2002年中国东北、华北、华东15个省级地区的居民家庭人均消费数据(不变价格)表2上市公司的投资与股票账面价值:N=20,T=4面板数据模型和stata软件应用举例面板数据模型的误差项由两部分组成:一部分是与个体观察单位有关的,它概括了所有影响被解释变量,但不随时间变化的因素,因此,面板数据模型也常常被成为非观测效应模型;另外一部分概括了随截面随时间而变化的不可观测因素,通常被成为特异性误差或特异扰动项面板模型选择:固定效应还是随机效应固定效
