
解耦控制系统.ppt

YY****。。






亲,该文档总共62页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

解耦控制所谓解耦控制系统.pptx
会计学跟踪问题问题描述定义yr(t)定常情形,即yr(t)=yr(常数)该增广系统的状态反馈控制率则闭环系统为定理1:如果存在Kx,Kq使Acl稳定,则在干扰信号w定常的情况下,系统输出y(t)可跟踪给定信号yr。实际上由(2)得所以由Acl稳定得到受控系统为希望设计控制律使得y(t)跟踪给定信号yr(t),其中yr(t)由下述参考模型生成以上参考模型既可代表所要设计的控制系统的希望相应特性,又可代表被跟踪对象的模型。设计控制律定理2:设(A,B)可控,如果存在矩阵G,H满足那么对任何一个能使原系统稳定(

解耦控制系统.ppt
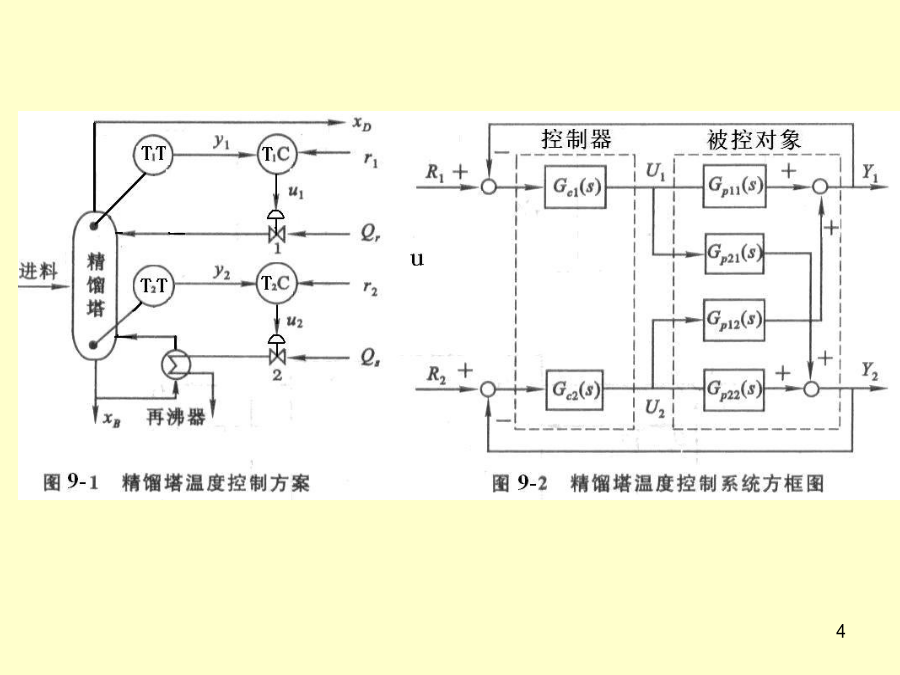
第9章解耦控制系统前面所讨论的控制系统中,假设过程只有一个被控变量(即输出量),在影响这个被控变量的诸多因素中,仅选择一个控制变量(即输入量),而把其它因素都看成扰动,这样的系统就是所谓的单输入单输出系统。但实际的工业过程是复杂的,往往有多个过程参数需要进行控制,影响这些参数的控制变量也不只有一个,这样的系统称之为多输入多输出系统。当多输入多输出系统中输入和输出之间相互影响较强时,不能简单地化为多个单输入单输出系统,此时必须考虑到变量间的耦合,以便对系统采取相应的解耦措施后再实施有效的控制。9.1解耦控制

解耦控制系统.ppt
第9章解耦控制系统前面所讨论的控制系统中,假设过程只有一个被控变量(即输出量),在影响这个被控变量的诸多因素中,仅选择一个控制变量(即输入量),而把其它因素都看成扰动,这样的系统就是所谓的单输入单输出系统。但实际的工业过程是复杂的,往往有多个过程参数需要进行控制,影响这些参数的控制变量也不只有一个,这样的系统称之为多输入多输出系统。当多输入多输出系统中输入和输出之间相互影响较强时,不能简单地化为多个单输入单输出系统,此时必须考虑到变量间的耦合,以便对系统采取相应的解耦措施后再实施有效的控制。9.1解耦控制

解耦控制系统.ppt
解耦控制系统学习内容1耦合过程及其要解决的问题2相对增益与相对增益矩阵3解耦控制系统的设计1.耦合过程及其要解决的问题令某一通道在其它系统均为开环时的放大系数与该一通道在其它系统均为闭环时的放大系数之比为λij,称为相对增益;相对增益λij是Uj相对于过程中其他调节量对该被控量Yi而言的增益(Uj→Yi);λij定义为第一放大系数pij(开环增益)指耦合系统中,除Uj到Yi通道外,其它通道全部断开时所得到的Uj到Yi通道的静态增益;即,调节量Uj改变了Uj所得到的Yi的变化量Yi与Uj之比,其它调节

解耦控制系统.ppt
解耦控制学习内容1耦合过程及其要解决的问题2相对增益与相对增益矩阵3解耦控制系统的设计1.耦合过程及其要解决的问题令某一通道在其它系统均为开环时的放大系数与该一通道在其它系统均为闭环时的放大系数之比为λij,称为相对增益;相对增益λij是Uj相对于过程中其他调节量对该被控量Yi而言的增益(Uj→Yi);λij定义为第一放大系数pij(开环增益)指耦合系统中,除Uj到Yi通道外,其它通道全部断开时所得到的Uj到Yi通道的静态增益;即,调节量Uj改变了Uj所得到的Yi的变化量Yi与Uj之比,其它调节量U
