
实验三统计回归模型Matlab求解.docx

快乐****蜜蜂









在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

实验三统计回归模型Matlab求解.docx
实验三:统计回归模型Matlab求解一、实验目的[1]通过范例学习建立统计回归的数学模型以及求解全过程;[2]熟悉MATLAB求解统计回归模型的过程。二、实验原理问题:一家技术公司人事部门为研究软件开发人员的薪金与他们的资历、管理责任、教育程度等因素之间的关系,要建立一个数学模型,以便分析公司人事策略的合理性,并作为新聘用人员薪金的参考。他们认为目前公司人员的薪金总体上是合理的,可以作为建模的依据,于是调查来46名软件开发人员的档案资料,如表4,其中资历一列指从事专业工作的年数,管理一列中1表示管理人员,

用MATLAB求解回归分析.ppt
数学建模与数学实验实验目的一元线性回归一、数学模型一元线性回归分析的主要任务是:二、模型参数估计其中返回三、检验、预测与控制(Ⅰ)F检验法(Ⅲ)r检验法2、回归系数的置信区间3、预测与控制(2)控制四、可线性化的一元非线性回归(曲线回归)散点图通常选择的六类曲线如下:一、数学模型及定义二、模型参数估计返回三、多元线性回归中的检验与预测2、预测四、逐步回归分析这个过程反复进行,直至既无不显著的变量从回归方程中剔除,又无显著变量可引入回归方程时为止。统计工具箱中的回归分析命令多元线性回归3、画出残差及其置信区

实验四 用MATLAB求解状态空间模型.docx
实验四用MATLAB求解状态空间模型1、实验设备MATLAB软件2、实验目的①学习线性定常连续系统的状态空间模型求解、掌握MATLAB中关于求解该模型的主要函数;②通过编程、上机调试,进行求解。3、实验原理说明Matlab提供了非常丰富的线性定常连续系统的状态空间模型求解(即系统运动轨迹的计算)的功能,主要的函数有:初始状态响应函数initial()、阶跃响应函数step()以及可计算任意输入的系统响应数值计算函数lsim()和符号计算函数sym_lsim()。数值计算问题可由基本的Matlab函数完成,
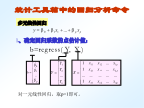
用MATLAB求解回归分析 (2).ppt
多元线性回归3、画出残差及其置信区间:rcoplot(r,rint)例13、残差分析,作残差图:rcoplot(r,rint)方法一法二(二)多元二项式回归例3设某商品的需求量与消费者的平均收入、商品价格的统计数据如下,建立回归模型,预测平均收入为1000、价格为6时的商品需求量.在画面左下方的下拉式菜单中选”all”,则beta、rmse和residuals都传送到Matlab工作区中.在Matlab工作区中输入命令:beta,rmse结果为:b=110.53130.1464-26.5709-0.000

导弹追击模型-matlab求解.doc
《数学软件与数学实验》课程设计实验题目导弹追击问题数学实验报告实验名称导弹追击问题课程设计问题背景描述:某军的一导弹基地发现正北方向200km处海面上有敌舰一艘以100km/h的速度向正东方向行驶.该基地立即发射导弹跟踪追击敌舰,导弹速度为500km/h,自动导航系统使导弹在任一时刻都能对准敌舰.实验目的与任务:(1)试问导弹在何时何处击中敌舰?(2)如果当基地发射导弹的同时,敌舰立即由仪器发觉.假定敌舰为一高速快艇,它即刻以150km/h的速度与导弹方向垂直的方向逃逸,问导弹何时何地击中敌舰?(3)如果
