第2章 随机信号及其时域统计特性.ppt

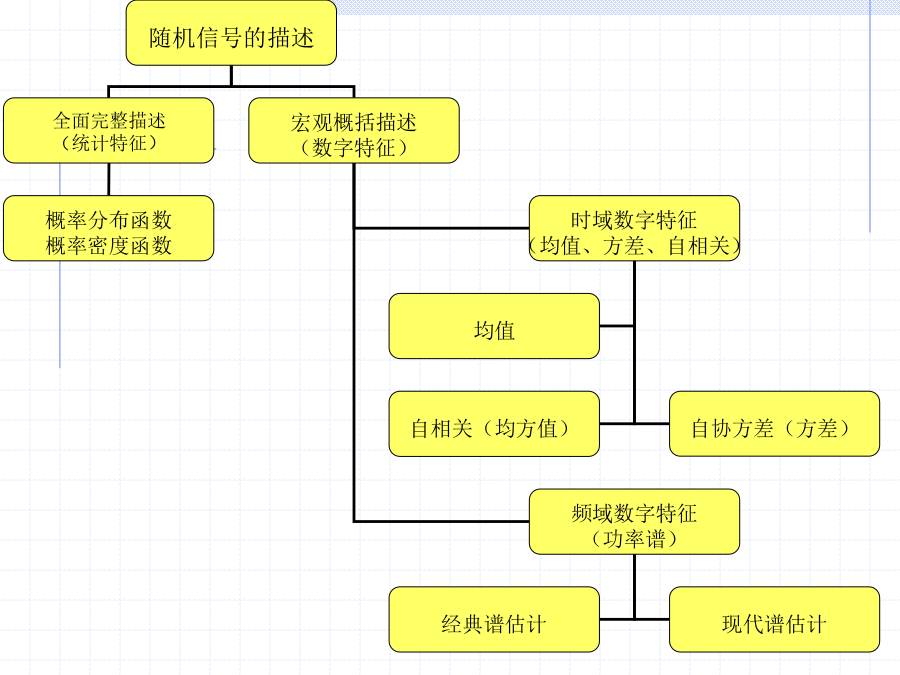
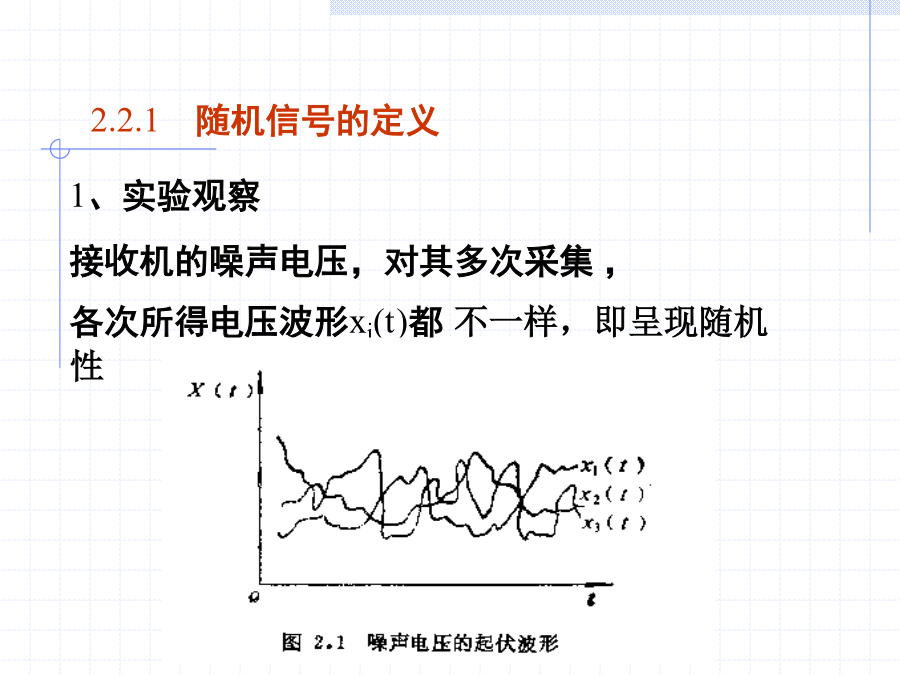
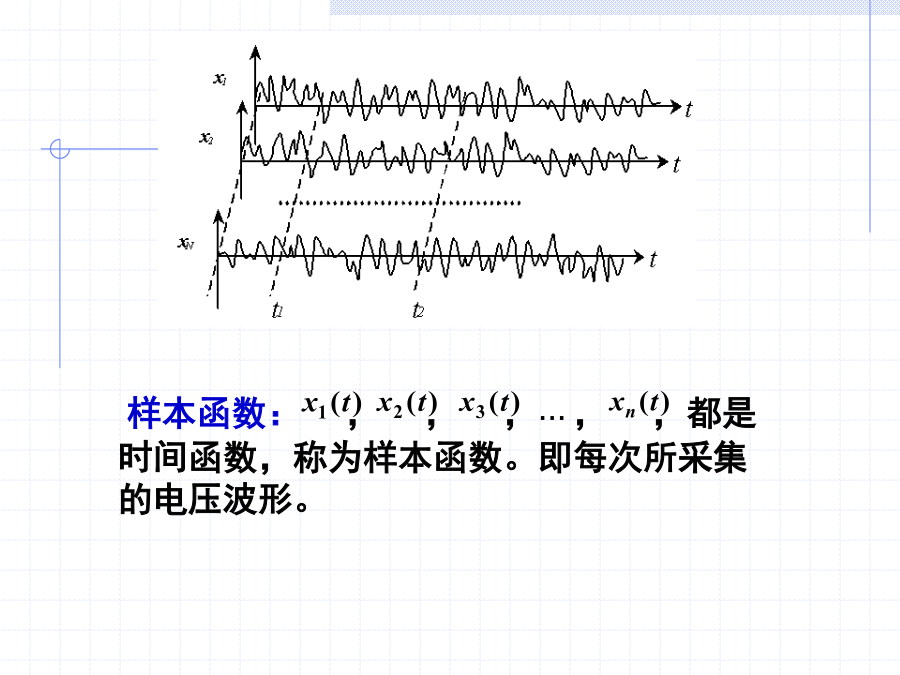
第二章2.12.2.1随机信号的定义样本函数：，，，…，，都是时间函数，称为样本函数。即每次所采集的电压波形。2.由实验角度对随机信号下定义3.定义的理解：随机变量例1设具有随机初始相位的正弦波2.2.2分类离散型随机序列2.按样本函数的形式来分类例2设随机信号定义为：例3离散型随机信号的样本函数皆为常数，
即X(t)=C=可变常数，其中C为随机变量，其可能值
为C1=1，C2=2和C3=3，它们分别已概率0.6、0.3及0.1
出现。X(t)是确定性随机信号吗？3.其他分类2.2.3随机信号的概率分布2.二维概率分布函数和二维概率密度函数3.n维概率分布函数和n维概率密度函数4.概率分布函数和概率密度函数的性质概率密度函数与概率分布函数的应用利用振幅频次分布研究设备的随机疲劳和载荷谱
振幅峰图(a)：上升的峰值A
振幅频次图(b)：横座标--振幅峰，纵座标--振幅峰在观测时间内出现的频次。即动态波形峰值出现的频次分布。
累计频次图(c)：对图(b)沿横坐标进行累计。
图(b)和(c)即随机载荷谱。

随机载荷谱可用于判断材料所要具备的耐受程度概率密度函数用于机器状态判断
新变速箱噪声的概率密度曲线如图(a)所示，旧变速箱噪声的概率密度曲线如图(b)所示2.2.5随机信号的数字特征1.数学期望（一阶原点矩）2.均方值（二阶原点矩）和方差（二阶中心矩）物理意义：如果表示噪声电压，则均方值和方差分别表示单位电阻上的瞬时功率的统计平均值；单位电阻上的瞬时交流功率的统计平均值。时域参数3.自相关函数
注意有些书标为Rxx(t1,t2)/Rx(t1,t2)

自相关函数用来描述随机信号任意两个时刻的状态之间的内在联系，通常用描述。自相关函数及其应用自相关函数及其应用自相关函数及其应用自相关分析诊断的实例自相关分析诊断的实例4.自协方差函数
注意有些书标为COVxx(t1,t2)/Cxx(t1,t2)/Cx(t1,t2)自协方差和自相关函数的关系设两个随机信号和，它们在任意两个时刻t1，t2的取值为随机变量、,则定义它们的互相关函数为：
互相关函数的性质如下互相关分析的应用实例互相关分析的应用实例3、两个随机信号间的三种基本统计关系t1,t2都具有或，
(1)相互独立(二阶矩都存在)→两者不相关。

(2)正态随机信号：不相关=相互独立。
举例（2）方差（3）自相关函数例4：求随机相位正弦波的数学期望，方差，自相关函数及一维概率密度。式中，为常数，是区间[0，]上均匀分布的随机变量。例5：设随机信号X(t)=A+Bt，其中A和B是相互独立的正态分布N(0,1)随机变量，求X(t)的数学期望、方差、自相关函数、协方差函数、一维和二维概率密度函数。（3）自相关函数（5）一维概率密度函数（6）二维概率密度函数例6(课堂练习)：设随机信号X(t)=Acosw0t，其中w0为常数，A为在(0,1)之间均匀分布的随机变量，
(1)画出随机信号X(t)的几个样本函数图形；
(2)试求t=0、π/(4w0)和3π/(4w0)时，X(t)的一维概率密度函数。
(3)求X(t)的均值、相关函数、协方差函数和方差函数例6(课堂练习)：设随机信号X(t)=Acosw0t，其中w0为常数，A为在(0,1)之间均匀分布的随机变量，2.1.7时域统计特性的小结2.2随机信号的微分和积分一、连续性的定义2.随机信号的连续性3.随机信号的相关函数连续，则连续二、微分（求导数）2.随机信号的可导如果随机信号满足随机信号X(t)在t处均方可微的充分条件为：相关函数在它的自变量相等时，存在二阶混合偏导数且连续，即存在3.数字特征例2.随机信号X(t)的数学期望为例2.随机信号X(t)的数学期望为三、随机信号的积分2.随机信号的积分③加权积分：3.定区间随机信号积分的数字特征(1)积分的数学期望=数学期望的积分积分的举例(2)求Y(t)的均值、自相关函数和自协方差函数基本要求：1.严平稳随机信号(2)一、二维概率密度及数学特征严平稳随机信号的二维概率密度只与t1,t2的时间间隔有关，而与时间起点无关(3)严平稳的判断若随机信号X(t)满足例2.设随机信号Z(t)=Xsint+Ycost，其中X和Y是相互独立的
二元随机变量，它们都分别以2/3和1/3的概率取-1和2，试求：
Z(t)的均值和自相关函数；
证明Z(t)是宽平稳的，但不是严平稳的。因此，Z(t)不是严平稳的。例2.设随机信号X(t)=t2+Asint+Bcost，其中A和B都是一元随机变
量，且E[A]=E[B]=0，D[A]=D[B]=10，E[AB]=0，试分别讨论
X(t)和Y(t)=X(t)-mX(t)的平稳性。性质1性质4平稳随机信号必须满足对所有均成立。严平稳随机信号此值在[－1，1]之间。相关时间例4：