
第1章 随机信号概论(特征函数随机过程统计特性).doc

kp****93








在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

第1章 随机信号概论(特征函数随机过程统计特性).doc
1.4随机变量的特征函数引言:分布函数:反映随机变量的统计规律性。数字特征:反映、掌握分布函数的某些特征。矩是最主要的特征,但随着矩的阶数的增高,计算机较麻烦,寻求一种有效的方法来计算。特征函数:一种计算各阶矩的有效工具。特别是计算、处理多个随机变量,特征函数显示其优越性一。1.4.1特征函数的定义(1)设是定义在概率空间上的随机变量,它的分布函数为,称的数学期望为的特征函数,记为。当为离散型随机变量时,其特征函数为:当为连续型随机变量时,其特征函数为:(2)利用特征函数求

《随机过程》教程第12讲 随机信号的正交分解.ppt
《随机过程》教程第12讲随机信号的正交分解内容提要正交分解和随机信号的表示正交分解随机信号的Fourier正交分解随机信号的K-L正交分解2024/8/82024/8/82024/8/8作业《随机过程》第12讲“随机信号的正交分解”终。
第2章 随机信号及其时域统计特性.ppt
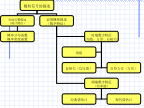
第二章2.12.2.1随机信号的定义样本函数:,,,…,,都是时间函数,称为样本函数。即每次所采集的电压波形。2.由实验角度对随机信号下定义3.定义的理解:随机变量例1设具有随机初始相位的正弦波2.2.2分类离散型随机序列2.按样本函数的形式来分类例2设随机信号定义为:例3离散型随机信号的样本函数皆为常数,即X(t)=C=可变常数,其中C为随机变量,其可能值为C1=1,C2=2和C3=3,它们分别已概率0.6、0.3及0.1出现。X(t)是确定性随机信号吗?3.其他分类2.2.3随机信号的概率分布2.二维

随机信号分析-1 随机过程(1).ppt
随机信号分析234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859宽平稳随机过程61626364656667平稳随机过程相关函数性质697071727374757677787980818283848586878889909192939495复随机过程及其数字特征复随机过程及其数字特征复随机过程及其数字特征复随机过程及其数字特征复随机过程及其数字特

随机过程的基本概念以统计特性.pptx
会计学23456789101112131415161718192021222324252627282930313233343536373839404142434445464849
