
力法李廉锟结构力学中南大学.pptx

胜利****实阿








亲,该文档总共206页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

力法李廉锟结构力学中南大学.pptx
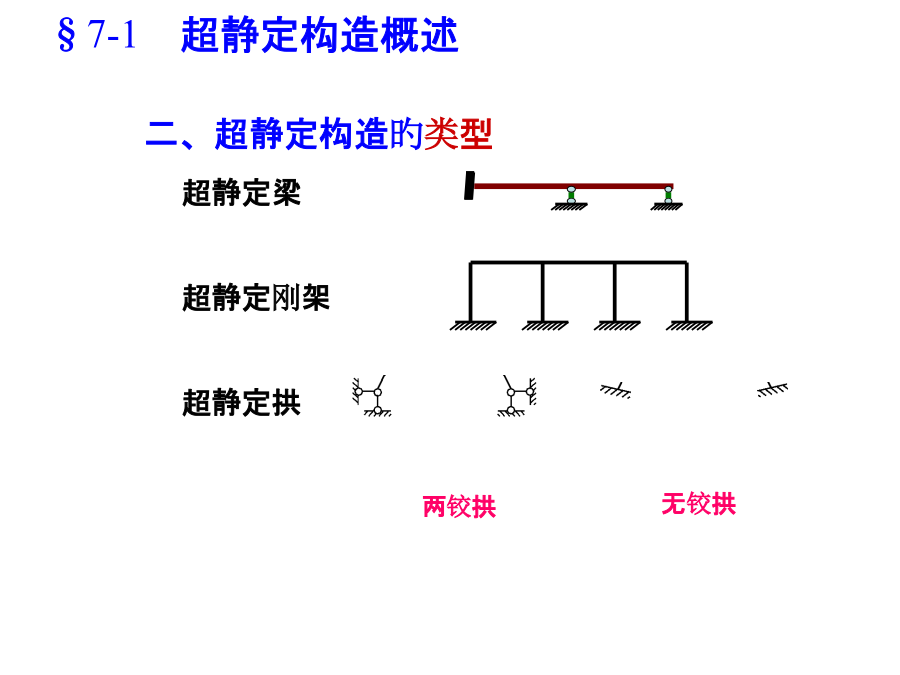
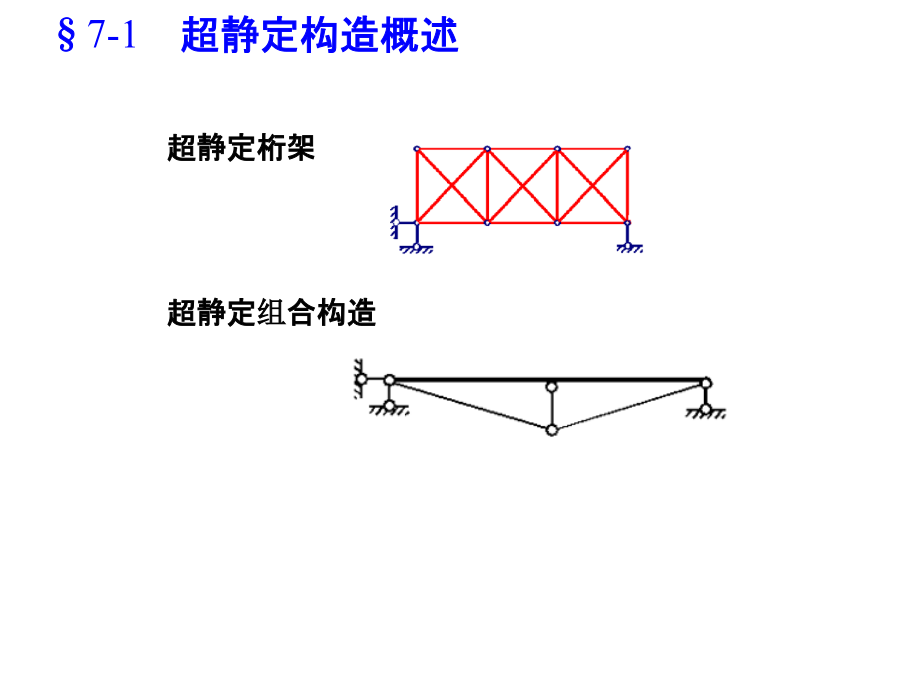
第七章力法§7-8最终内力图旳校核超静定构造:具有多出约束旳构造。思索:多出约束是多出旳吗?二、超静定构造旳类型超静定桁架MethodsofAnalysisofStaticallyIndeterminateStructures以位移作为基本未知量,在自动满足变形协调条件旳基础上来分析,当然这时主要需处理平衡问题,这种分析措施称为位移法(displacementmethod)。4.力矩分配法----近似计算措施超静定次数:多出约束(联络)或基本未知力旳个数。解除多出约束旳方法拟定超静定构造旳超静定次数,应注

结构力学李廉锟 答案.pdf
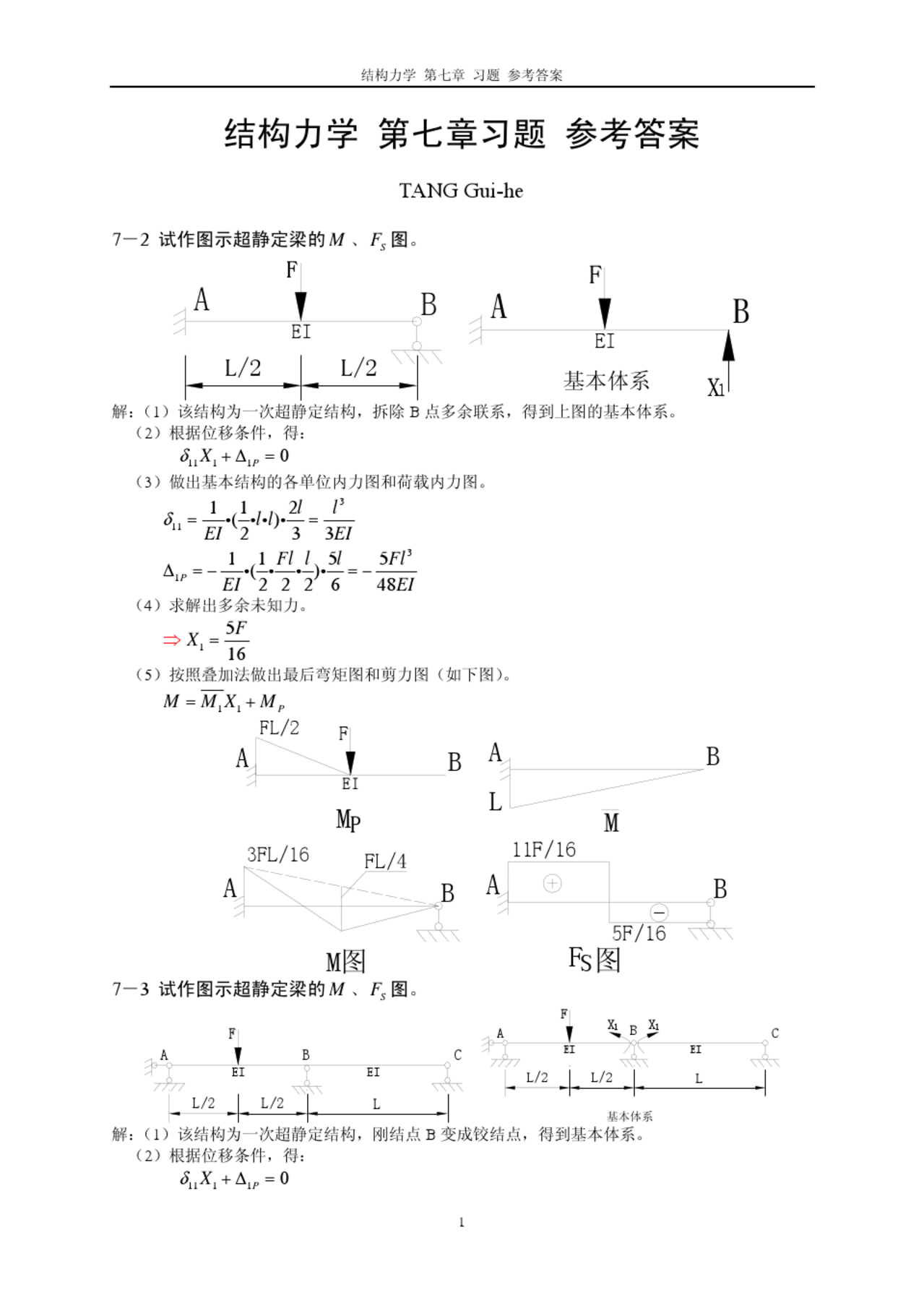
结构力学第七章习题参考答案结构力学第七章习题参考答案TANGGui-he7-2试作图示超静定梁的M、F图。SFFABABEIEIL/2L/2基本体系X1解:(1)该结构为一次超静定结构,拆除B点多余联系,得到上图的基本体系。(2)根据位移条件,得:δX+Δ=01111P(3)做出基本结构的各单位内力图和荷载内力图。112ll3δ=i(ilil)i=11EI233EI11Fll5l5Fl3Δ=−i(ii)i=−1PEI222648EI(4)求解出多余未知力。5F⇒X=116(5)按照叠加法做出最后弯矩图和剪

结构力学李廉锟结构位移计算讲义.pptx
会计学A截面C、D的相对竖向线位移为:A铁路工程技术规范规定:(2)超静定结构、动力和稳定计算的基础(3)理想联结(IdealConstraint)。本章只讨论应用虚功原理求解结构位移。一、基本概念实功的数值就等于图上三角形OAB的面积。实功是外力的非线形函数,计算外力实功不能应用叠加原理。2.外力的虚功力F1在力F2引起的位移Δ12上作的功为虚功为——结构产生的各种位移,包括截面的线位移、角位移、相对线位移、相对角位移或者是一组位移等等都可泛称为广义位移。4.内力功如果变形就是由此内力引起的,则此微段上

影响线及其应用李廉锟-结构力学.pptx
第十一章影响线及其应用§11-9最不利荷载位置移动荷载:荷载大小、方向不变,荷载作用点随时间改变,结构所产生加速度的反应与静荷载反应相比可以忽略,这种特殊的作用荷载称移动荷载。(车辆荷载、人群荷载、吊车荷载等)在结构分析和设计中,必须解决以下问题:—数字和量纲均为1,可以在实际移动荷载可到达的范围内移动。在研究移动荷载作用所产生的影响时,只要把单位移动荷载作用下对某量值的影响分析清楚,根据叠加原理,可求得各种实际移动荷载对该量值的影响。3.根据函数关系,绘制出该量值的影响线。若影响线为正值,则绘于y轴正向
结构力学李廉锟 第七章 答案.pdf
