
专题复习《线段和差最值问题》.doc

xf****65





在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

专题复习:《线段和差最值问题》.doc
线段和差最值问题评测练习谷城县石花镇第一中学李绍平合作探究一如图,在抛物线的对称轴上找一点P,使点P到点B与点C的距离之和最小,求出点P的坐标.变式如图,在抛物线的对称轴上找一点P,使PA–PC的值最大,求出点P的坐标.合作探究二如图,CF=BC,E是AB中点,在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.拓展如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN

专题复习《线段和差最值问题》.doc
《线段和差最值问题》教学设计谷城县石花镇第一中学李绍平一、教学目标1.了解解决线段和差最值问题的基本策略和基本原理;2.训练学生运用以上基本策略和基本原理解决坐标系、抛物线、三角形、四边形、圆等知识相关的线段和差最值问题;3.通过解决问题培养学生转化问题的能力,以及及时总结反思的良好习惯.二、学情分析从心理特点来看,九年级的学生思想成熟,有想法,对直观事物的感知能力强,想象力丰富,正逐步从形象思维过渡到抽象思维.在知识储备上,他们在八年级上册已经学习过《最短路径问题》,对坐标系、抛物线、三角形、四边形、圆

中考专题复习——线段和差最值问题.doc
中考专题复习——线段和差最值问题一、考点分析:“两点之间线段最短”、“垂线段最短”。考的较多的还是“饮马问题”,出题背景变式有角、三角形、菱形、矩形、正方形、圆、坐标轴、抛物线等。二、教学目标:1、理解并掌握实际生活中最短问题的实质就是垂线段最短、两点之间,线段最短;2、巩固、提高空间观念、模型思想和几何直观的思想和意识。三、重点、难点分析:教学重点:借助三大变换转移线段达到共线的目的。教学难点:①正确合理的添加辅助线,寻找解决问题的方法;②通过探索解决问题的过程,进行方法的归纳和建模,形成解决问题的通法

线段和差最值问题.pdf
.专题一.线段和〔差的最值问题[知识依据]1.线段公理——两点之间线段最短;2.对称的性质——①关于一条直线对称的两个图形全等;②对称轴是两个对称图形对应点连线的垂直平分线;3.三角形两边之和大于第三边;4.三角形两边之差小于第三边;5、垂直线段最短。一、已知两个定点:1、在一条直线m上求一点P使PA+PB最小;〔1点A、
线段和差最值问题.doc
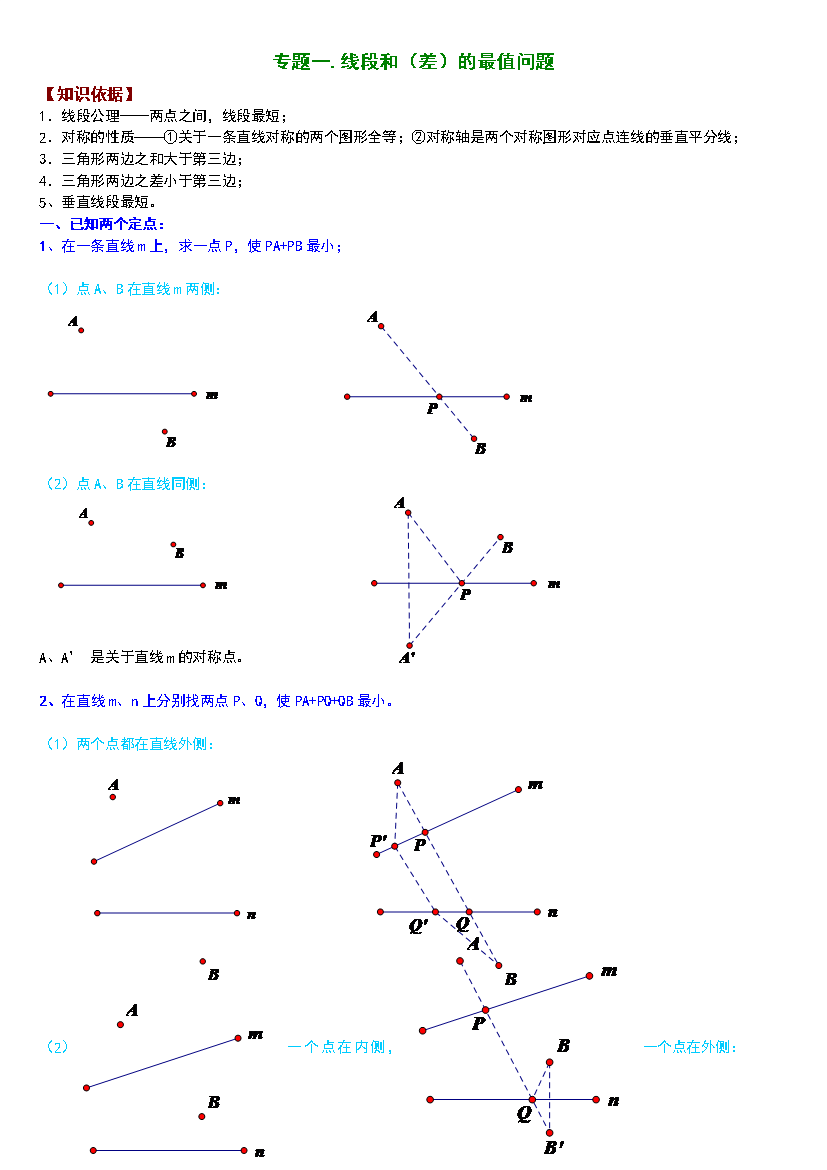
专题一.线段和(差)的最值问题【知识依据】线段公理——两点之间,线段最短;对称的性质——①关于一条直线对称的两个图形全等;②对称轴是两个对称图形对应点连线的垂直平分线;三角形两边之和大于第三边;三角形两边之差小于第三边;垂直线段最短。一、已知两个定点:1、在一条直线m上,求一点P,使PA+PB最小;(1)点A、B在直线m两侧:(2)点A、B在直线同侧:A、A’是关于直线m的对称点。2、在直线m、n上分别找两点P、Q,使PA+PQ+QB最小。(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)
