新QC7种道具.ppt

第二部分：新ＱＣ7种工具的目的新QC7种工具是在QC7种工具的基础上追加提案出的。
它是以语言数据解析为中心。
但是其中包含了手法之一的矩阵图（可以灵活的运用在数值数据方面）和其作为解析手段的矩阵解析法（数值数据的解析法）。
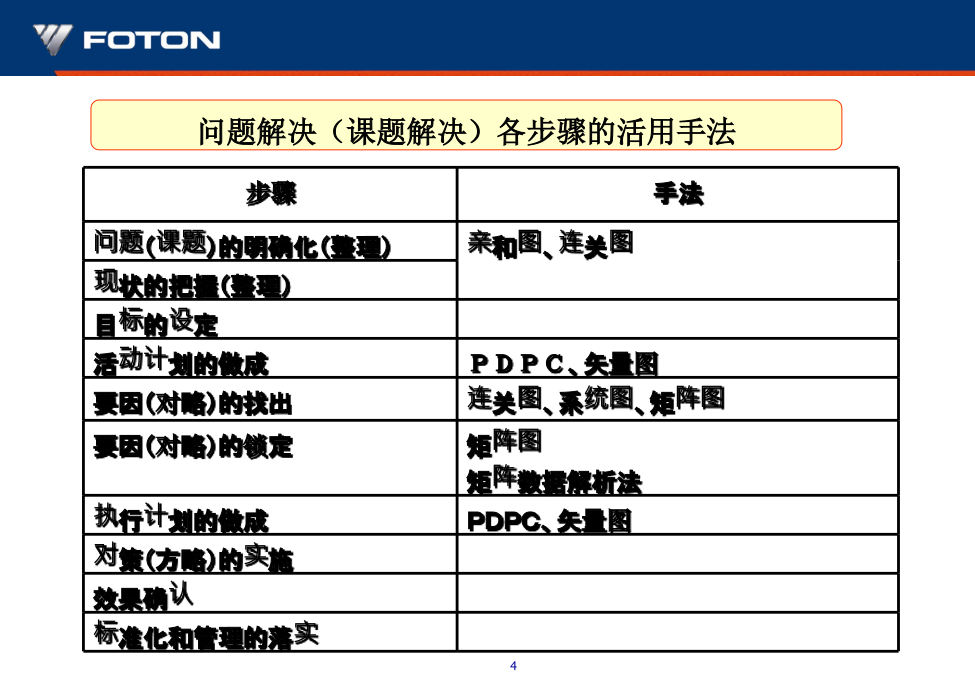
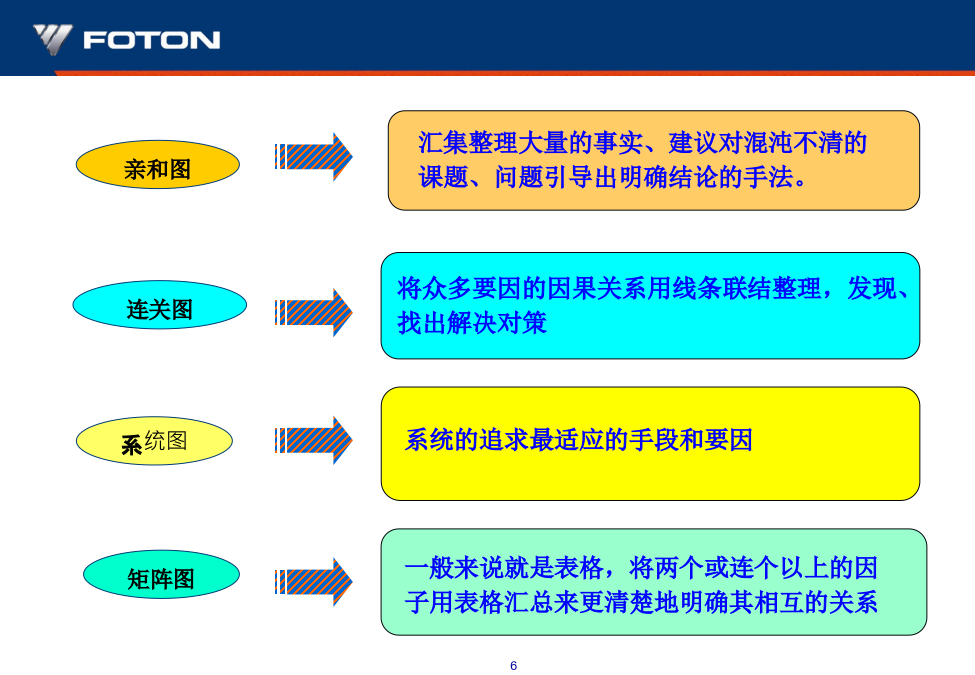
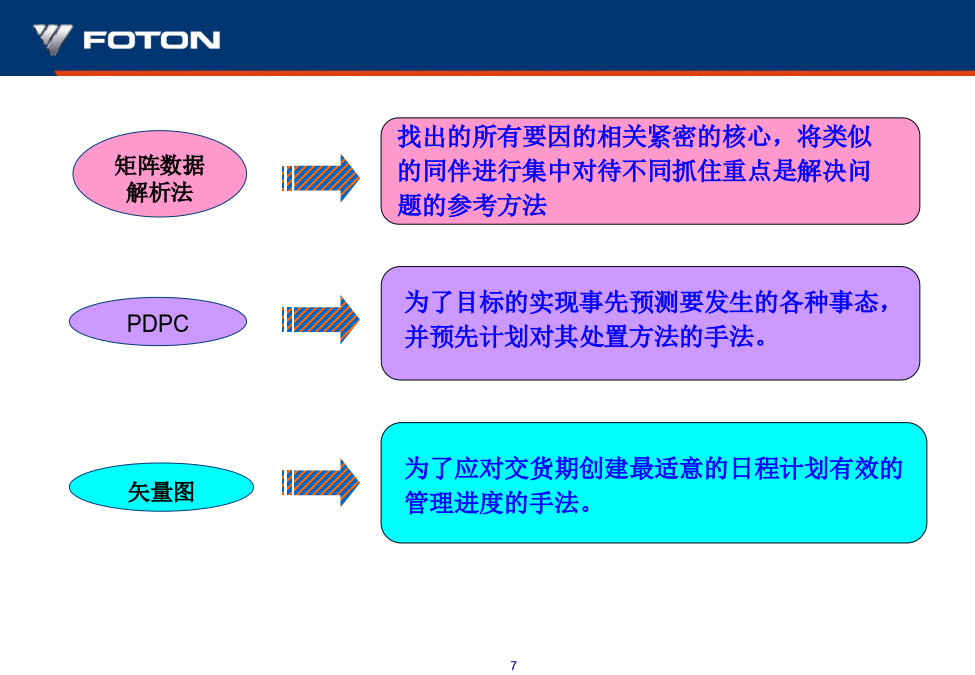
新QC7种工具可以灵活的运用在问题解决、课题解决方面，也可以作为管理方面课题的活用、有效的手法。问题解决（课题解决）各步骤的活用手法第二部分：新ＱＣ7种工具的目的汇集整理大量的事实、建议对混沌不清的课题、问题引导出明确结论的手法。为了应对交货期创建最适意的日程计划有效的管理进度的手法。第二部分：新ＱＣ7种工具的目的1、亲和图1.2灵活运用和有效事例
①不是听取个别客户的意见，而是将更多的意见进行整理，最合适的进行提案。
例：产品开发、商品开发、
②就各种活动的推进方法从相关人员中听取意见进行整理，把最合适的活动方法进行提案。
活动例：小团队活动
③进行业务改善时，从关联人员处收集意见找出最好的方法语言数据ａ１1顺序１确定题目

顺序２将事实、讲义填入卡中
用具体的容易理解的文章
一张卡上不能有两种建议

顺序３内容相似的卡排列在一起
感觉相似的卡收集在一起。没有相似的一张也行。

顺序４做成亲和卡
将收集的卡全部展示出来、具体的做成容易理解的文章。

顺序５根据需要进一步的收集亲和卡
做出更高层次的亲和卡

顺序６从这些亲和卡中引导出结论1.4亲和图法的实例：「要成为质量提升活动的带头人」事例：「提高商改的准确率」2、连关图问题点顺序１确定问题点

顺序２将考虑到的原因写成卡片

顺序３按照顺序宣读卡片，将因果关系强的就近放置

顺序４其中认为与问题最接近的作为第一要因放置在问题点最近
的地方

顺序５所有卡片｢原因→結果｣的关系都要用尖头连接

顺序６找出主要原因

顺序７汇总结论2.4连关图法的事例
「为什么新产品生产开始时的质量问题多」（体制上的问题）事例：「提升商改的准确率」3、系统图3.2灵活的运用和有效的事例
①在实行质量提升、成本降低、交货期缩短等活动时，对应目标应该怎样做进行检讨。
②发生质量问题时通过[为什么、为什么]来推定原因。
③为了满足顾客的需求将产品的性能、功能进行明示。3.3做成顺序
1)可问题解决得情况下：顺序１确定题目

顺序２确认题目的课题、目的

顺序３考虑一次手段
课题作为目的考虑手段

顺序４展开二次以后的手段
手段作为目的考虑以后的手段る

顺序５确认目的和课题和手段的关系
确认内容是否背离

顺序６选出手段中重要的东西2）解决问题的场合手順１题目确定

手順２确认问题点

手順３考虑一次要因

手順４展开二次以后的要因
手段作为目的考虑以后的手段

手順５确认问题点与要因的关系
确认内容是否背离

手順６选出手段中重要的东西・・・・・・2）解决问题的场合
「新产品生产开始时组装问题多」与驾驶员的位置关系材料強度4.1直方图的特征
(1)所谓的矩阵图法就是我们都知道的表格。
表中相互对照的要素配置成行与列，通过对有无关联、关联的程度有效的解决问题的推进手法。
(2)要素有三种以上的场合可以用3维或T型配置表示做出表格。
4.2适用的问题
①新产品开发时对应客户的要求质量和质量特性（质量表）。
②从复数的目的和复数的手段的关系中找出重点。
③系统图展开结果的重要度通过复数的评价指标来决定。
4.3做成顺序：详细省略。
纵轴（行）和横轴（列）上配置找出的项目。
纵轴（行）和横轴（列）的项目内容（表现手法）及交点的重量记入的内容要根据目的来决定。4.4矩阵图法的事例
「３Ｃ评价矩阵图」与系统图的结合制定出能够使顾客满意的设计质量，该设计意图要展开到制造工序。质量功能展开表是所提供产品在设计阶段以质量保证为目的的研究手法。
代表性的模版是系统图和矩阵图的组合。以下是做出的事例（顺序）。
①将顾客的要求置换到系统图的各部分功能当中去具体化。
②明确矩阵图横轴上记载的图面上诸要素和①中具体化要求功能的关联
便于看出来的形状⇒宽、厚度、・・・
依此为基准确保设计、试验评价、制造的质量。质量展开概略图例5.2主要用途如下：
1.分析含有复杂因素的工序；
2.从大量数据中分析不良品的原因；
3.从市场调查的数据中把握要求质量，进行产品市场定位分析；
4.感官特性的分类系统化；
5.复杂的质量评价；
6.对应曲线的数据分析
5.3原理（只介绍概要・・・计算顺序省略）
矩阵图中被整理数据因子数的空间中片加结构。（P38页的事例中6次元・・・现实当中无法实现数学上可以。）、向相关性最强的方向划线作为「第1主成分」。顺次在直角方向相关性强的方向方向划直线作为「第２主成分」、「第３主成分」・・・。
其结果、是相似的同类聚集将个别的数据中判定周的意义。（自我解释）。对某车型顾客问卷中让顾客就重