
“特殊化法”在高中数学选择题中的应用.docx

快乐****蜜蜂



在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

“特殊化法”在高中数学选择题中的应用.docx
“特殊化法”在高中数学选择题中的应用特殊化法在高中数学选择题中的应用引言:特殊化法是一种在数学问题中常用的解题方法,尤其常见于高中数学选择题中。它通过将问题中的变量特殊化,通过设定特定的条件或取特定的数值来简化问题,从而使复杂的问题变得更加易于解决。本文将探讨特殊化法在高中数学选择题中的应用,以及如何灵活运用这一方法来解决各种问题。一、特殊化法的基本思想与原理:特殊化法的基本思想是将问题中的变量特殊化,通过设定特定的条件或取特定的数值来简化问题。这是因为对于一些复杂的问题,我们往往难以一下子找到一般性的解

特殊化策略在高考选择题中的应用.docx
特殊化策略在高考选择题中的应用特殊化策略在高考选择题中的应用摘要:特殊化策略是一种在解决问题时从特殊情况到一般情况递推的思维策略。在高考选择题中,特殊化策略能够帮助考生更加有效地解题,提高答题效率和准确性。本文将从特殊化策略的概念、特点和运用等方面进行讨论,旨在帮助考生在高考中更好地运用特殊化策略解题。一、特殊化策略的概念与特点特殊化策略是指在解决问题(特别是数学问题)时,从特殊情况到一般情况递推的思维策略。其具体操作步骤为:首先找到一个特殊情况,然后通过观察和推理,找出特殊情况和一般情况之间的联系,最后

特殊化法在高考数学解题中的应用研究.docx
特殊化法在高考数学解题中的应用研究特殊化法是一种重要的数学思想方法美籍匈牙利数学家波利亚在其“怎样解题”表中就提到了特殊化的方法他在“怎样解题”表中提示我们:你若不能解这个问题试先解一个相关的问题.你能想出一个更容易着手的有关问题么?一个更一般的问题?一个更特殊的问题?特殊化法简单的说就是指在处理数学问题的过程中先讨论满足其条件的特殊情况以期达到或逐步达到一般性结果的思想方法.运用特殊化法解决数学问题往往能够使得数学问题趋于简单化、容易化而且特殊的情形对一般性问

特殊化法在高考数学解题中的应用研究.docx
特殊化法在高考数学解题中的应用研究特殊化法是一种重要的数学思想方法美籍匈牙利数学家波利亚在其“怎样解题”表中就提到了特殊化的方法他在“怎样解题”表中提示我们:你若不能解这个问题试先解一个相关的问题.你能想出一个更容易着手的有关问题么?一个更一般的问题?一个更特殊的问题?特殊化法简单的说就是指在处理数学问题的过程中先讨论满足其条件的特殊情况以期达到或逐步达到一般性结果的思想方法.运用特殊化法解决数学问题往往能够使得数学问题趋于简单化、容易化而且特殊的情形对一般性问
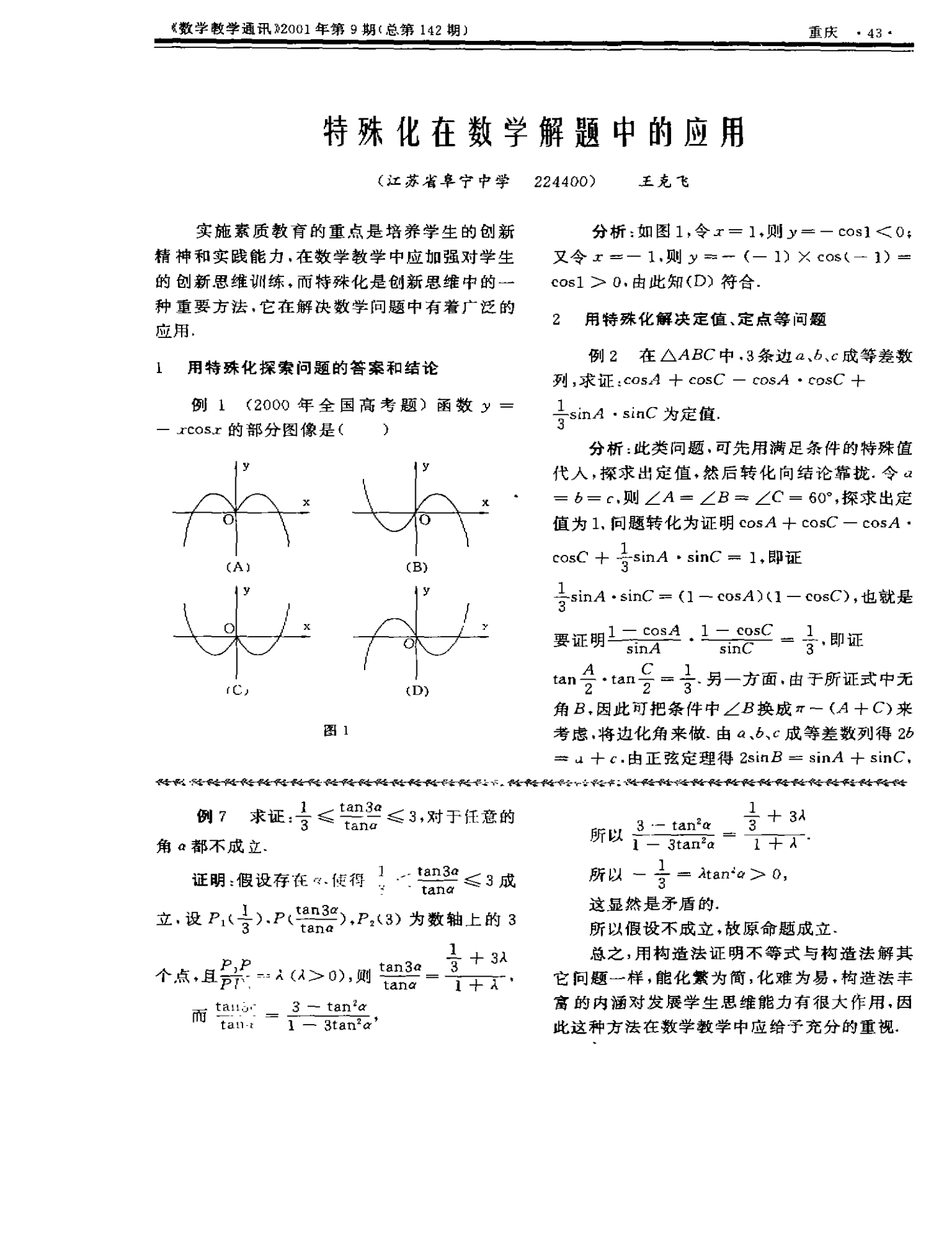
特殊化在数学解题中的应用.pdf
《数学教学通讯年第期总第期重庆··
