古典概型ppt课件.ppt

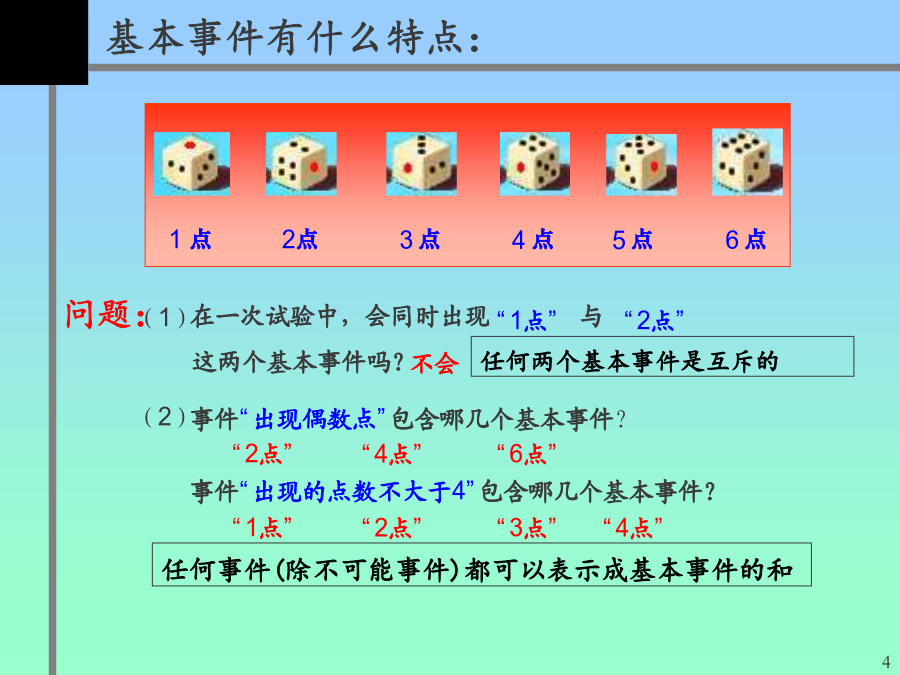
必修3考察两个试验：（2）掷一枚质地均匀的骰子，结果只有6个，即“1点”、“2点”、“3点”、“4点”、“5点”和“6点”.1例1从字母a、b、c、d任意取出两个不同字母的试验中，有哪些基本事件？1六个基本事件
的概率都是对于某些随机事件，也可以不通过大量重复实验，而只通过对一次实验中可能出现的结果的分析来计算概率。问题4：向一个圆面内随机地投射一个点，如果该点落在圆内任意一点都是等可能的，你认为这是古典概型吗？为什么？问题5：某同学随机地向一靶心进行射击，这一试验的结果有：“命中10环”、“命中9环”、“命中8环”、“命中7环”、“命中6环”、“命中5环”和“不中环”。
你认为这是古典概型吗？
为什么？掷一颗均匀的骰子,（A）同时抛掷两枚均匀的硬币，会出现几种结果？列举出来.例3、同时掷两个骰子，计算：
（1）一共有多少种不同的结果？
（2）其中向上的点数之和是5的结果有多少种？
（3）向上的点数之和是5的概率是多少？（6，6）为什么要把两个骰子标上记号？如果不标记号会出现什么情况？你能解释其中的原因吗？为什么要把两个骰子标上记号？如果不标记号会出现什么情况？你能解释其中的原因吗？因此，在投掷两个骰子的过程中，我们必须对两个骰子加以标号区分例3：假设储蓄卡的密码由4个数字组成，每个数字可以是0，1，2…，9十个数字中的任意一个。假设一个人完全忘记了自己的储蓄卡密码，问他到自动提款机上随机试一次密码就能取到钱的概
率是多少？解：这个人随机试一个密码，相当做1次随机试验，试验的基本事件（所有可能的结果）共有10000种，它们分别是0000，0001，0002，…，9998，9999.由于是随机地试密码，相当于试验的每一个结果试等可能的．所以例4：某种饮料每箱装6听，如果其中有2听不合格，问质检人员从中随机抽取2听，检测出不合格产品的概率有多大？练习1：某口袋内装有大小相同的5只球，其中3只白球，2只黑球，从中一次摸出2只球.
（1）共有多少个基本事件？
（2）摸出的2只球都是白球的概率是多少？
解（1）分别记白球为1，2，3号，黑球为4，5号，从中摸出2只球，有如下基本事件（摸到1，2号球用（1，2）表示）：
(1,2),(1,3),(1,4),(1,5),
(2,3),(2,4),(2,5),（3,4),
(3,5),(4,5).
因此，共有10个基本事件.
（2）如下图所示，上述10个基本事件的可能性相同，且只有3个基本事件是摸到2只白球（记为事件A），242.做投掷二颗骰子试验，用(x,y)表示结果，其中x表示第一
颗骰子出现的点数，y表示第二颗骰子出现的点数，求：
(1)事件“出现点数之和大于8”的概率是
(2)事件“出现点数相等”的概率是4.(2010·山东卷)一个袋中装有四个形状大小完全相同的球，球的编号分别为1,2,3,4.
(1)从袋中随机取两个球，求取出的球的编号之和不大于4的概率；
(2)先从袋中随机取一个球，该球的编号为m，将球放回袋中，然后再从袋中随机取一个球，该球的编号为n，
求n<m＋2的概率．27求古典概型概率的步骤:
⑴求基本事件的总数;
⑵求事件A包含的基本事件的个数;
⑶代入计算公式：