
排队论讲义.ppt

lj****88









亲,该文档总共99页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

排队论讲义.ppt
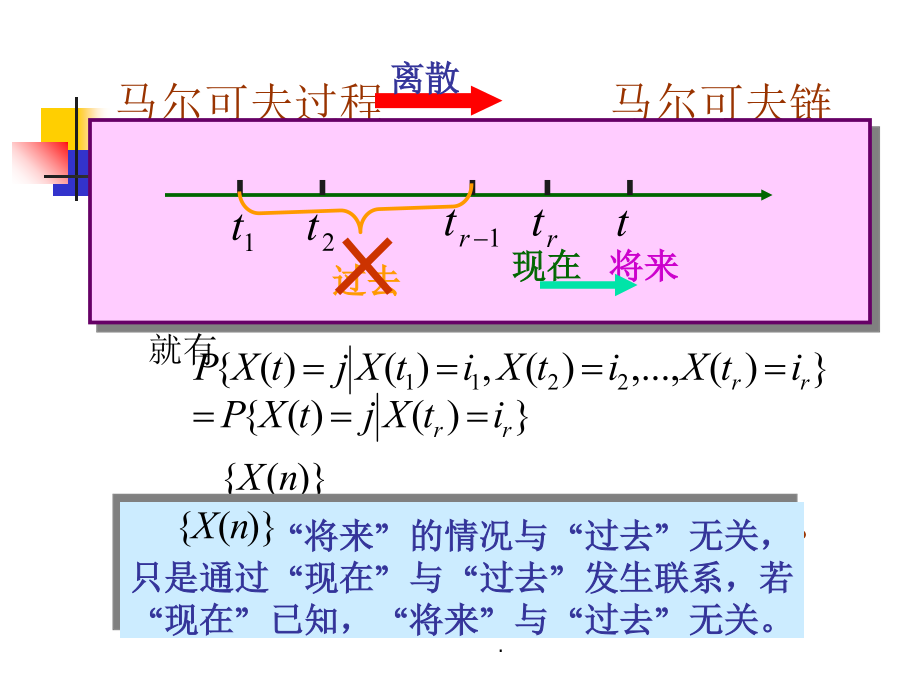
排队论一、概率论及随机过程回顾一、概率论及随机过程复习随机变量连续型随机变量概率密度函数概率分布函数数学期望和方差常见连续型随机变量的概率分布均匀分布指数分布?正态分布?k阶爱尔朗分布??爱尔朗分布1.2随机过程的有关概念随机过程的基本类型二阶矩过程平稳过程平稳独立增量过程常见随机过程马尔可夫过程?Poisson过程?生灭过程?定义:若满足如下性质:对任意非负整数,只要就有则称具有马尔可夫性,或无后效性。时齐的马氏链:马氏链若满足:则称为时齐马尔可夫链Poisson过程Poisson过程与Poisson分

排队论(讲义).ppt
排队论QueueingTheoryCONTENTSPREPARATION概率论和随机过程(2)相对频率定义:P(A)=limnA/nn→∞其中n是实验的次数,nA是A发生的次数例2投硬币在大数量投掷后,硬币的正面在上的可能性在0.5左右,上下两面在上面具有相同的概率。(3)公理化定义:从一定数量的定义概率度量的公理出发,经过推导规则达到概率的有效计算。这些公理包括:(a)对于每一个事件A,有0≤P(A)≤1(b)P(Ω)=1(c)如果A和B是互斥的,则P(AUB)=P(A)+P(B)3全概率公式和贝叶斯定

排队论讲义.ppt
排队论一、概率论及随机过程回顾一、概率论及随机过程复习随机变量连续型随机变量概率密度函数概率分布函数数学期望和方差常见连续型随机变量的概率分布均匀分布指数分布?正态分布?k阶爱尔朗分布??爱尔朗分布1.2随机过程的有关概念随机过程的基本类型二阶矩过程平稳过程平稳独立增量过程常见随机过程马尔可夫过程?Poisson过程?生灭过程?定义:若满足如下性质:对任意非负整数,只要就有则称具有马尔可夫性,或无后效性。时齐的马氏链:马氏链若满足:则称为时齐马尔可夫链Poisson过程Poisson过程与Poisson分

日化行业排队论与服务过程管理讲义.pptx
排队论与服务过程管理排队的实例服务方式排队系统实例:采购过程实例:晶片制造管理排队的建议(续)一个简单的排队模型简单的排队模型实例:M/M/1模型Little公式电话中心电话中心电话中心:超越传统的排队电话中心:超越传统的排队优化电话中心的人员配置优化人员配置服务质量(续)服务质量(续)服务质量电话中心的其它问题接电话并记下请求问题:周转时间很长。通常为6天,有时长达2周,尽管实际的处理时间只有90分钟。你如何解决这个问题?

珠宝行业排队论与服务过程管理讲义.pptx
排队论与服务过程管理排队的实例服务方式排队系统实例:采购过程实例:晶片制造管理排队的建议(续)一个简单的排队模型简单的排队模型实例:M/M/1模型Little公式电话中心电话中心电话中心:超越传统的排队电话中心:超越传统的排队优化电话中心的人员配置优化人员配置服务质量(续)服务质量(续)服务质量电话中心的其它问题接电话并记下请求问题:周转时间很长。通常为6天,有时长达2周,尽管实际的处理时间只有90分钟。你如何解决这个问题?9、静夜四无邻,荒居旧业贫。。11月-2411月-24Thursday,Novem
