
精品课件-连续信号与系统的频域分析PPT课件.ppt

lj****88






亲,该文档总共177页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

精品课件-连续信号与系统的频域分析PPT课件.ppt
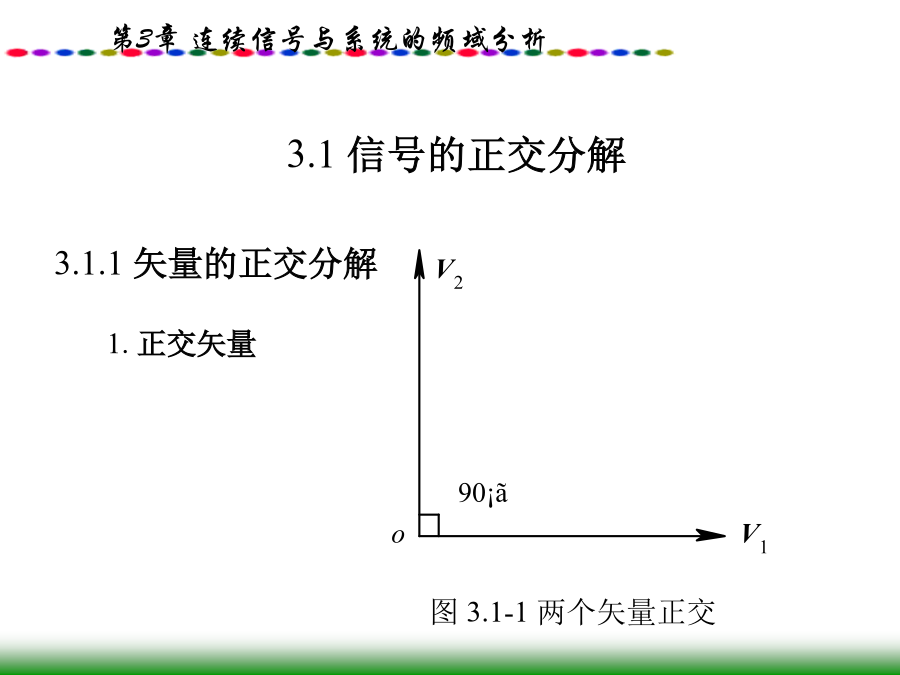
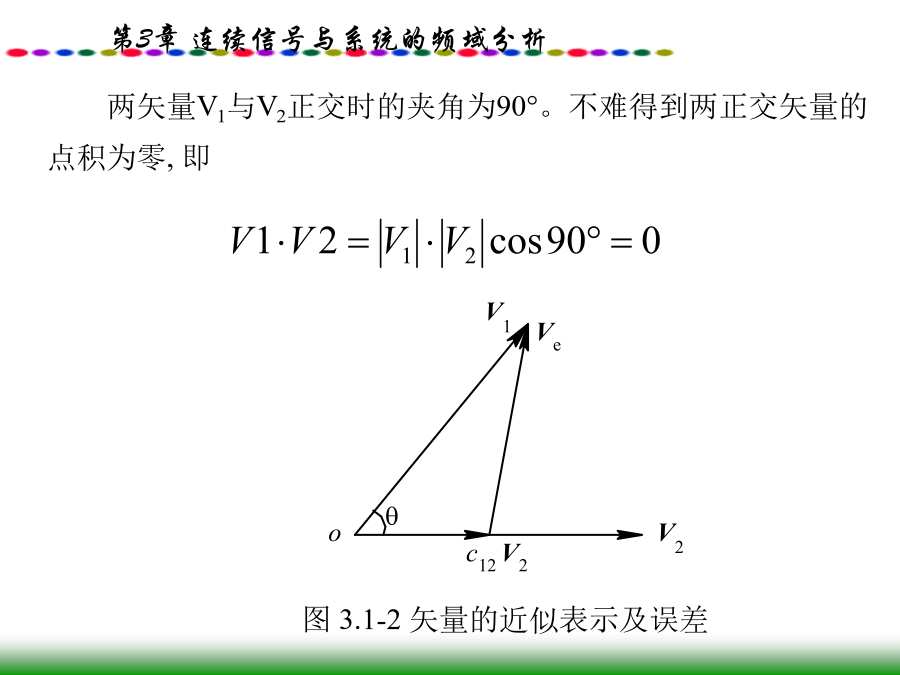
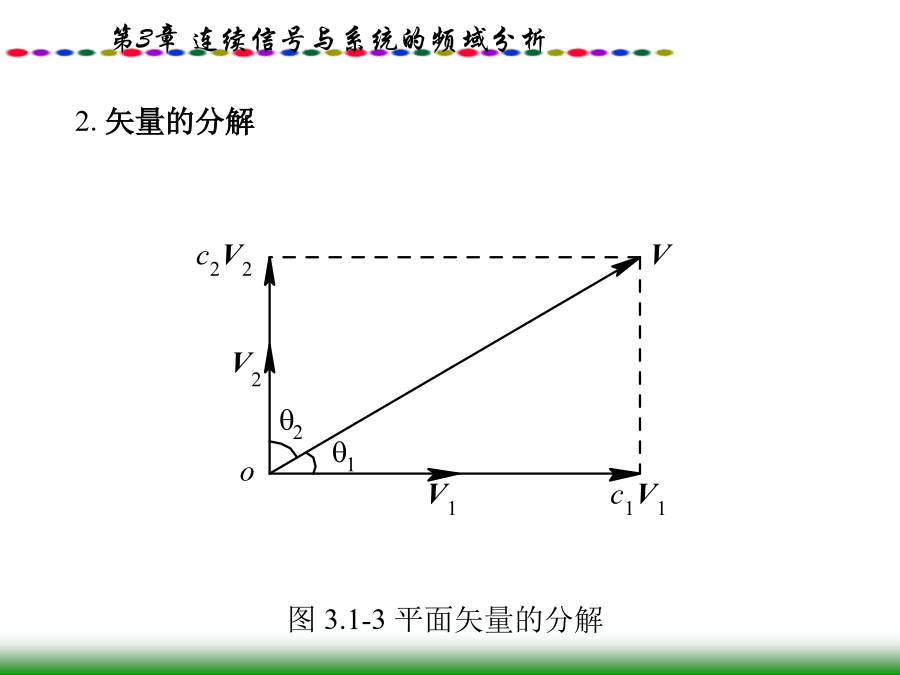
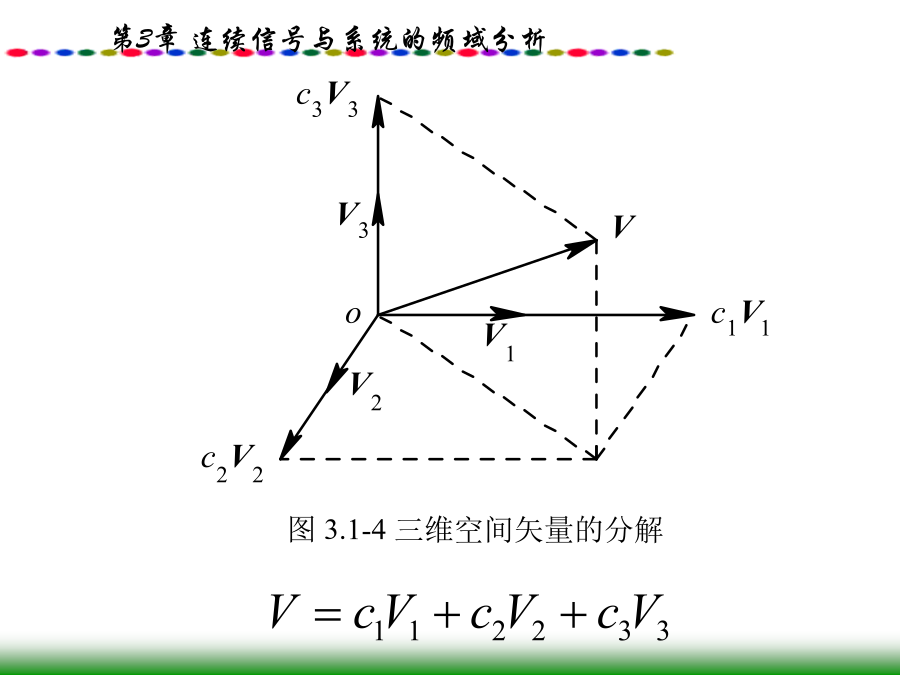
精品课件-连续信号与系统的频域分析3.0引言3.1信号的正交分解两矢量V1与V2正交时的夹角为90°。不难得到两正交矢量的点积为零,即所以最佳系数为若V1与V2正交,则θ=90°,cosθ=0,此时由式(3.1-2)得到的最佳系数c12=0。这表明当V1与V2正交时,用c12V2来近似表示V1还不如用0来近似V1。据此,我们可以把两个矢量V1与V2正交的概念解释如下:给定两个矢量V1和V2,现在要用与V2成比例的矢量c12V2近似地表示V1,要求误差矢量的模|Ve|最小(此时的c12称为最佳)。若最佳的

连续系统的频域分析PPT课件.ppt
连续系统的频域分析第四章连续系统的频域分析3456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108

信号与系统课件--5连续信号与系统复频域分析.ppt
第五章连续信号与系统复频域分析5-1连续信号拉普拉斯变换二、复平面(s平面)四、常用信号的单边拉氏变换(详见p169)五、拉氏变换基本性质2、尺度变换性:例3:求周期矩形脉冲信号的拉氏变换。4、频移性:解:9、时域卷积定理:初值:f(t)|t=0+=f(0+)例15-2拉普拉斯逆变换例1:例3:例4:留数法——回线积分法例5:例5(续)练习:5-3系统复频域分析3、电容元件5、模拟单元二、s域电路基本定律三、电路s域分析应用举例:图示电路,t<0,开关k闭合,电路稳定;t=0时k打开。求t>0时电路响应i

精品课件-连续信号与系统的时域分析PPT课件.ppt
精品课件-连续信号与系统的时域分析2.0引言2.1连续时间基本信号2.1.2正弦信号图2.1–1正弦信号正弦信号是周期信号,其周期T、频率f和角频率ω之间的关系为2.1.3指数信号图2.1–2实指数信号(2)若A=1,s=jω,则f(t)为虚指数信号,即(3)当A和s均为复数时,f(t)为复指数信号。若设A=|A|ejφ,s=σ+jω则f(t)可表示为图2.1–3复指数信号实部和虚部的波形2.2卷积积分即2.2.2卷积的图解机理第四步,将f1(τ)和f2(t-τ)相乘,得到卷积积分式中的被积函数f
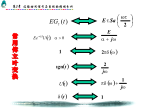
连续时间信号与系统的频域分析.ppt
常用傅立叶变换3.5连续时间系统的频域分析一、系统函数(传输函数):1、定义:2、求法:1)从定义求;2)从方程求;3)从冲激响应求;.4)从系统框图求;5)从电路图求.例:求系统函数H(j)。二、系统零状态响应:三、系统频率特性:MATLAB的计算机仿真:四、非周期信号激励下系统的零状态响应解题步骤例:五、系统全响应:六、周期信号通过线性系统2、正弦信号:3、任意周期信号:例:图示系统,若激励如图所示,求响应i(t)。练习:图示系统,频率特性如图所示,求响应y(t)。其中
