精品课件-连续信号与系统的时域分析PPT课件.ppt

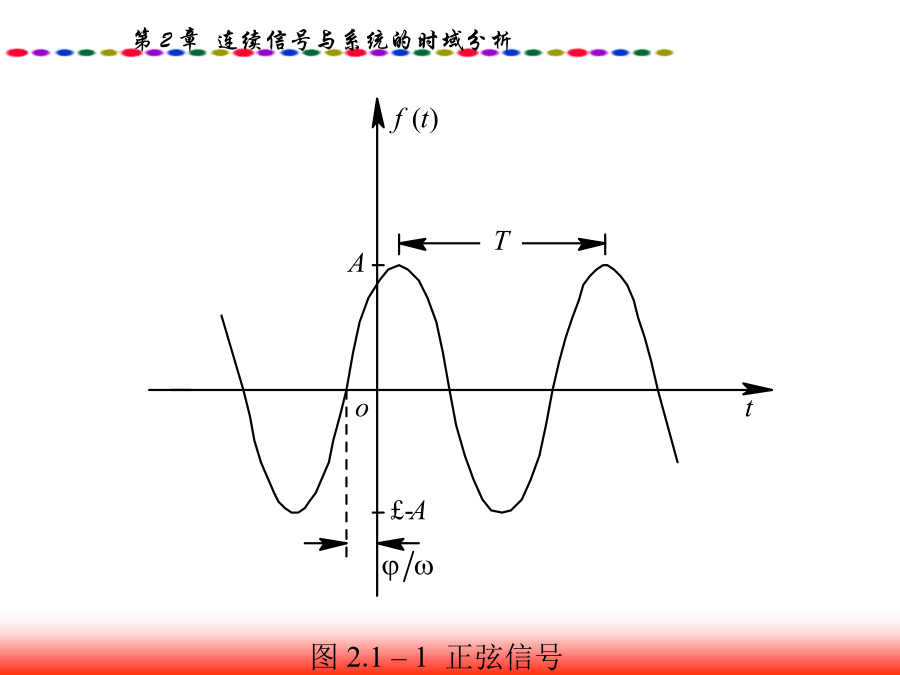
精品课件-连续信号与系统的时域分析2.0引言2.1连续时间基本信号2.1.2正弦信号图2.1–1正弦信号正弦信号是周期信号,其周期T、频率f和角频率ω之间的关系为2.1.3指数信号图2.1–2实指数信号(2)若A=1,s=jω,则f(t)为虚指数信号,即(3)当A和s均为复数时,f(t)为复指数信号。若设
A=|A|ejφ, s=σ+jω
则f(t)可表示为图2.1–3复指数信号实部和虚部的波形2.2卷积积分即2.2.2卷积的图解机理第四步,将f1(τ)和f2(t-τ)相乘,得到卷积积分式中的被积函数f1(τ)f2(t-τ)。
第五步,计算乘积信号f1(τ)f2(t-τ)波形与τ轴之间包含的净面积,便是式(2.2-1)卷积在t时刻的值。
第六步,令变量t在(-∞,∞)范围内变化,重复第三、四、五步操作,最终得到卷积信号f1(t)*f2(t)。例2.2–1给定信号图2.2–2卷积的图解表示当t<0时,f2(t-τ)波形如图2.2-2(c)所示,对任一τ,乘积f1(τ)f2(t-τ)恒为零,故y(t)=0。
当0<t<3时,f2(t-)波形如图2.2-2(d)所示。当t>3时,f2(t-τ)波形如图2.2-2(e)所示,此时,仅在0<τ<3范围内,乘积f1(τ)f2(t-τ)不为零,故有2.2.3卷积性质性质2f(t)与奇异信号的卷积
(1)信号f(t)与冲激信号δ(t)的卷积等于f(t)本身,即(2)信号f(t)与冲激偶δ′(t)的卷积等于f(t)的导函数,即(3)信号f(t)与阶跃信号ε(t)的卷积等于信号f(t)的积分,即性质3卷积的微分和积分(2)应用式(2.2-8)及卷积运算的结合律,可得(3)因为同理,可将f2(t)表示为对另一个函数进行k次积分的情况,即性质4卷积时移由卷积时移性质还可进一步得到如下推论:例2.2–2计算常数K与信号f(t)的卷积积分。
解直接按卷积定义,可得例2.2–3计算下列卷积积分:解(1)先计算ε(t)*ε(t)。因为ε(-∞)=0,故可应用卷积运算的微积分性质求得(2)利用卷积运算的分配律和时移性质,可将给定的卷积计算式表示为(3)由于图2.2–3例2.2-3图图2.2–4应用δT(t)产生周期信号例2.2–4图2.2-5(a)所示为门函数,在电子技术中常称矩形脉冲,用符号gτ(t)表示,其幅度为1,宽度为τ,求卷积积分gτ(t)*gτ(t)。图2.2–5例2.2-4方法一图方法二应用卷积运算的微积分和时移性质,可得图2.2–6例2.2-4方法二图2.2.4常用信号的卷积公式2.3系统的微分算子方程性质1以p的正幂多项式出现的运算式,在形式上可以像代数多项式那样进行展开和因式分解。例如:性质3微分算子方程等号两边p的公因式不能随便消去。例如,由下面方程性质42.3.2LTI系统的微分算子方程它代表了系统将输入转变为输出的作用,或系统对输入的传输作用,故称H(p)为响应y(t)对激励f(t)的传输算子或系统的传输算子。图2.3–1用H(p)表示的系统输入输出模型例2.3–1设某连续系统的传输算子为解选图中右端积分器的输出为中间变量x(t),则其输入为x′(t),左端积分器的输入为x″(t),如图所示。写出左端加法器的输出求得图2.3-2系统的微分方程为2.3.3电路系统算子方程的建立例2.3–3电路如图2.3-3(a)所示,试写出u1(t)对f(t)的传输算子。解画出算子模型电路如图2.3-3(b)所示。由节点电压法列出u1(t)的方程为例2.3–4如图2.3-4(a)所示电路,电路输入为f(t),输出为i2(t),试建立该电路的输入输出算子方程。解画出算子模型电路如图2.3-4(b)所示。列出网孔电流方程如下:该方程组对新设变量而言是一个微分方程组,可以用代数方法求解,得2.4连续系统的零输入响应对于因果系统,由于激励在t=0时接入,故有yf(0-)=0;对于时不变系统,内部参数不随时间变化,故有yx(0+)=yx(0-)。因此,式(2.4-2)和式(2.4-3)可改写为2.4.2零输入响应算子方程
设系统响应y(t)对输入f(t)的传输算子为H(p),且2.4.3简单系统的零输入响应式中,c0=yx(0-),其值由初始条件yx(0-)确定。因此,可得结论为简单系统2若A(p)=(p-λ)2,则yx(t)=(c0+c1t)eλt。两边乘以e-λt,再取积分2.4.4一般系统的零输入响应根据线性微分方程解的结构定理,令i=1,2,….,l,将相应方程求
和,便得第二步,求出第i个根对应的零输入响应yxi(t)某例2.4–1某系统输入输出微分算子方程为其一阶和二阶导函数为代入初始条件值并整理得例2.4-2电路如图2.4-1(a)所示,激励为is(t),响应为iL(t)。已知R1