
地震波运动学第四节---09级多层介质反射波时距曲线1ppt课件.ppt

lj****88






亲,该文档总共47页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

地震波运动学第四节---09级多层介质反射波时距曲线1ppt课件.ppt
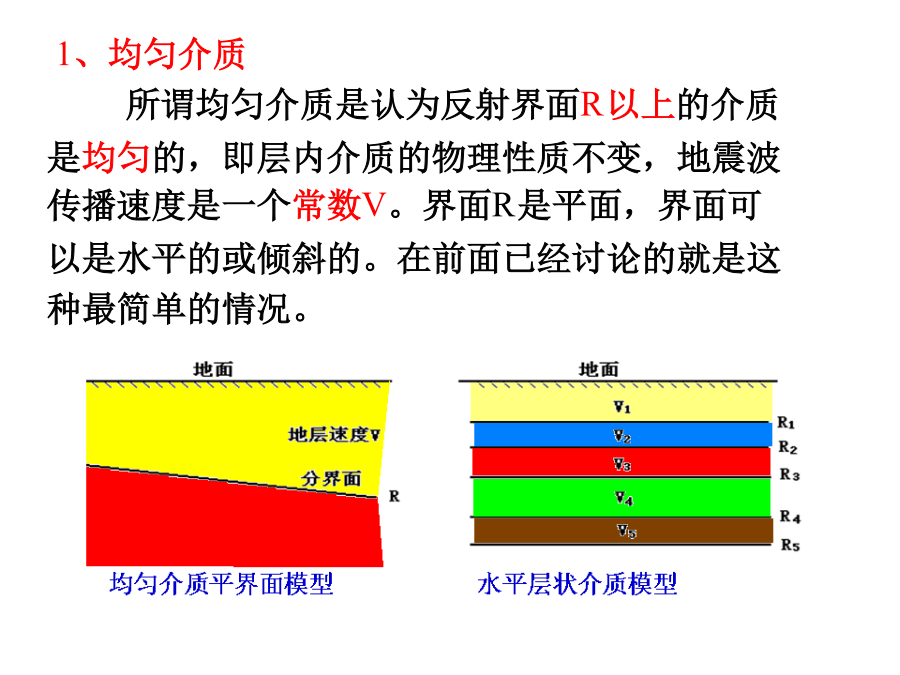
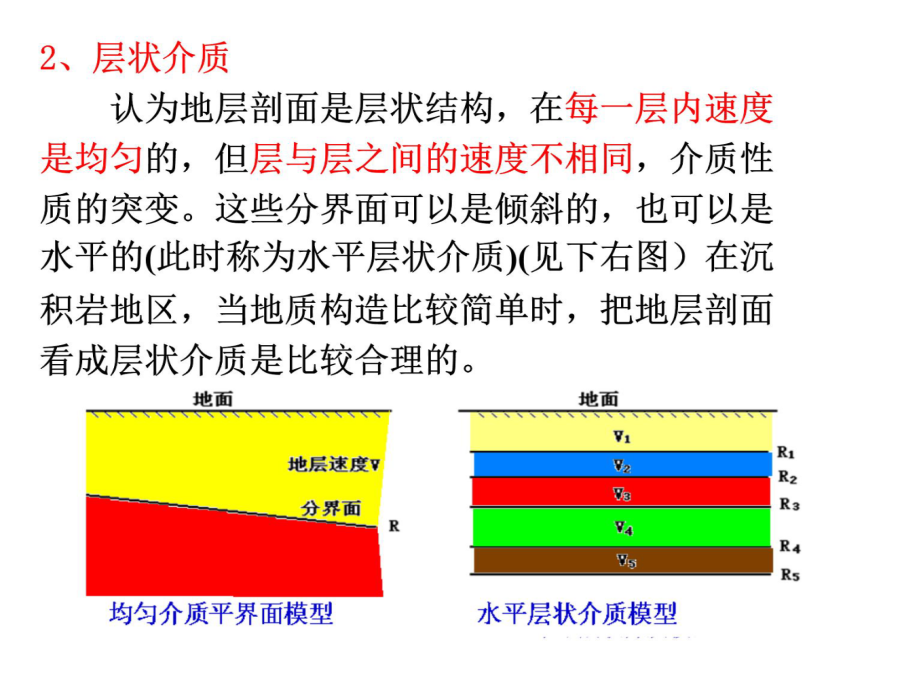
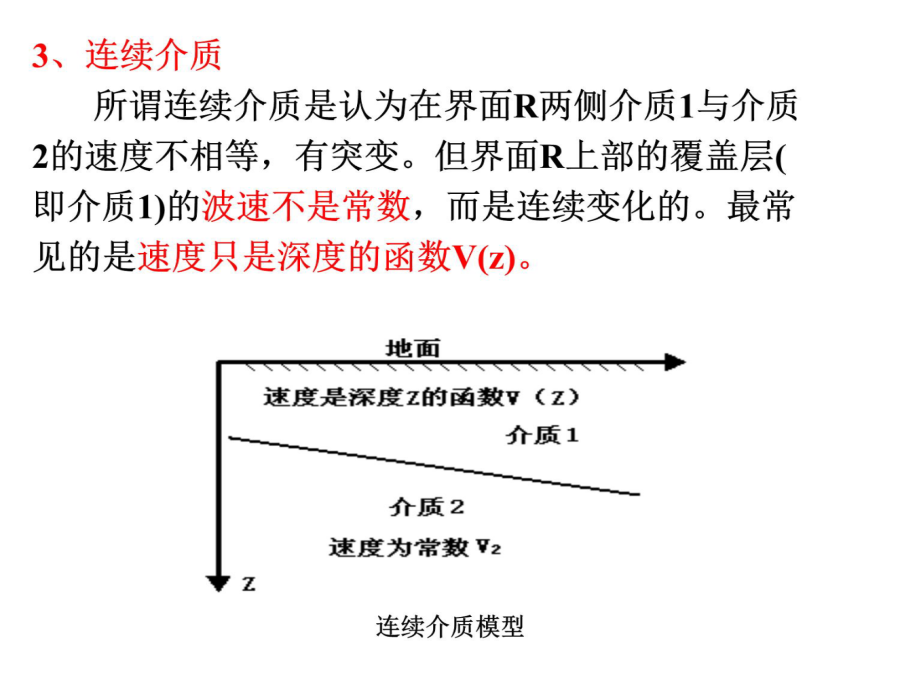
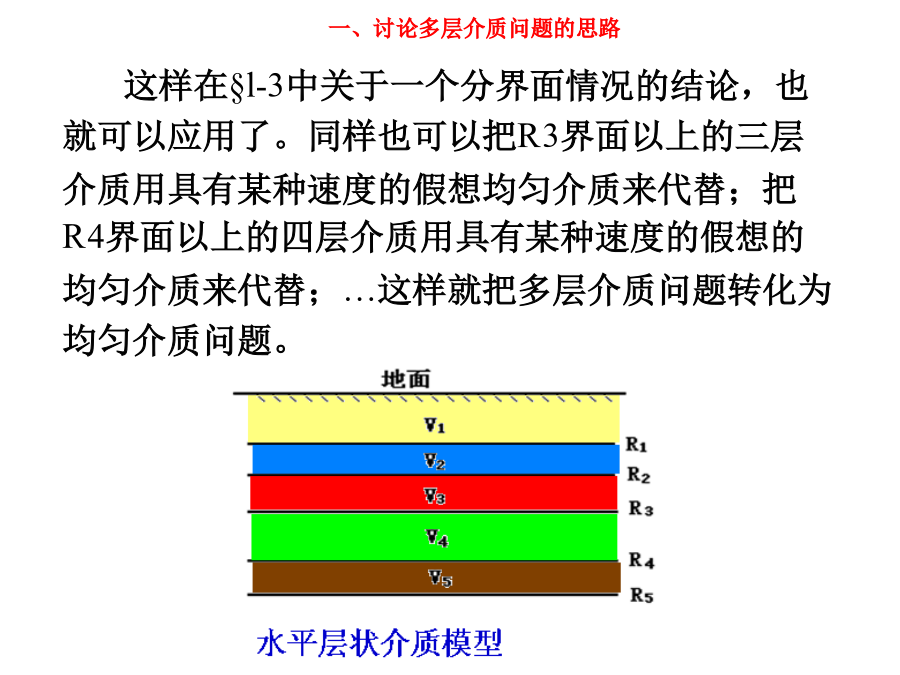
第四节多层介质反射波时距曲线Section4MultilayerMediumRefelectedWaveTimeDistanceCurve主要内容一、讨论多层介质问题的思路对同一类事物,这种模型可能是比较简单的,也可能是比较复杂的。简单的模型对客观事物的反映比较粗糙,由这种模型导出的一套分析问题进行计算的方法会比较简单、方便、但得出的结果精度较低。反之,较复杂的模型能更精确地反映实际事物,但往往会导致一套比较复杂的分析、计算方法。在地震勘探中对客观存在复杂的地层剖面,根据对问题研究的深入程度,对成果精度的

地震波运动学第四节---(09级)多层介质反射波时距曲线1.ppt
第四节多层介质反射波时距曲线Section4MultilayerMediumRefelectedWaveTimeDistanceCurve主要内容一、讨论多层介质问题的思路对同一类事物,这种模型可能是比较简单的,也可能是比较复杂的。简单的模型对客观事物的反映比较粗糙,由这种模型导出的一套分析问题进行计算的方法会比较简单、方便、但得出的结果精度较低。反之,较复杂的模型能更精确地反映实际事物,但往往会导致一套比较复杂的分析、计算方法。在地震勘探中对客观存在复杂的地层剖面,根据对问题研究的深入程度,对成果精度的

地震波运动学3——单界面反射波时距曲线.ppt
第三节单一界面反射波时距曲线Section3SingleRefelectedWaveTimeDistanceCurve主要内容1时距曲线概念要注意,这个距离x一般不是波传播的实际路程的长度,对沿测线传播的直达波,接收点相对于激发点的距离也就是直达波传播路程的长度,但对来自地下界面的反射波,就不是这样。直达波时距曲线:在O点激发,沿测线在x1、x2、x3、x4等点上接收。如果在x-t直角坐标系里,把激发点作为坐标原点,横坐标x表示测线上各观测点到激发点的距离,纵坐标t表示直达波到达各观测点的传播时间(见下图

连续介质中波的时间场和反射波的时距曲线.docx
七、连续介质中波的时间场和反射波的时距曲线讨论连续介质的思路V=V(z)叫连续介质,用微分的思想,将连续介质分成很多厚度为△h的水平薄层,利用水平层状介质的有关结论,然后令△h→0,速度就变成了连续函数,层状介质便过渡为连续介质。0tz连续介质V=V(Z)中波的射线和等时线方程均匀介质中波的射线和等时线方程Oxα等时线射线z射线方程:(x,z的关系)等时线方程:(x,z,t的关系)连续介质中波的射线方程xdzα(z)dsdx射线z连续介质中波的等时线方程线性介质中波的射线和等时线方程射线方程将代入,得——

地震波理论时距曲线.pdf
