
振动理论基础.ppt

lj****88





亲,该文档总共71页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

振动理论基础.pptx
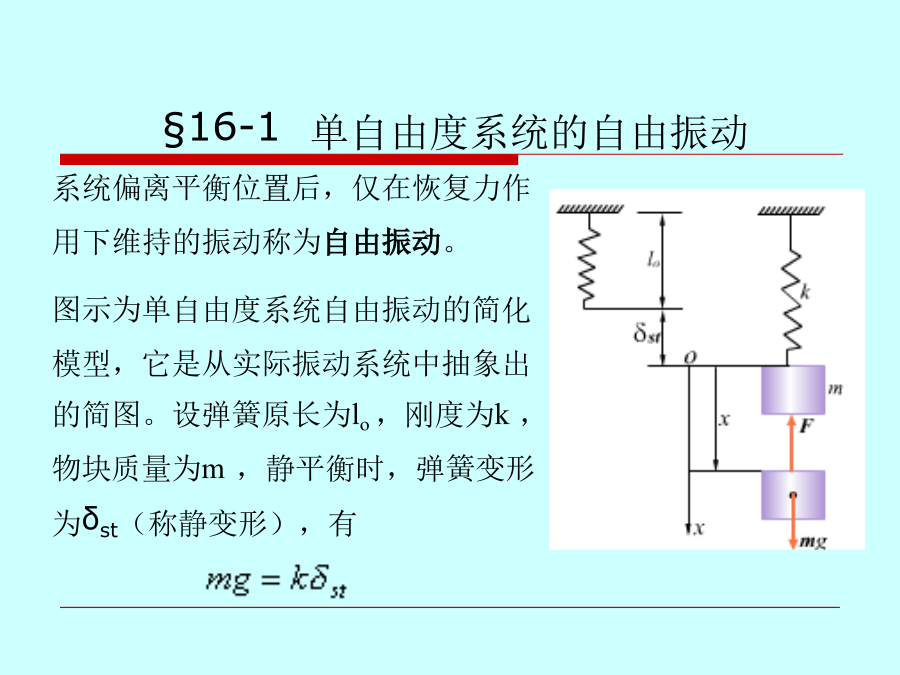
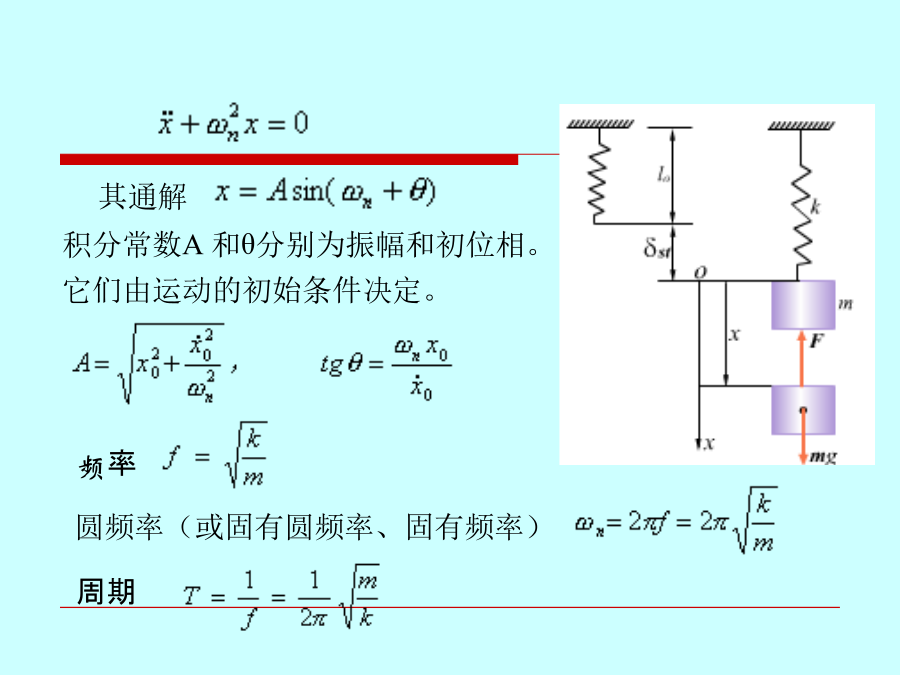
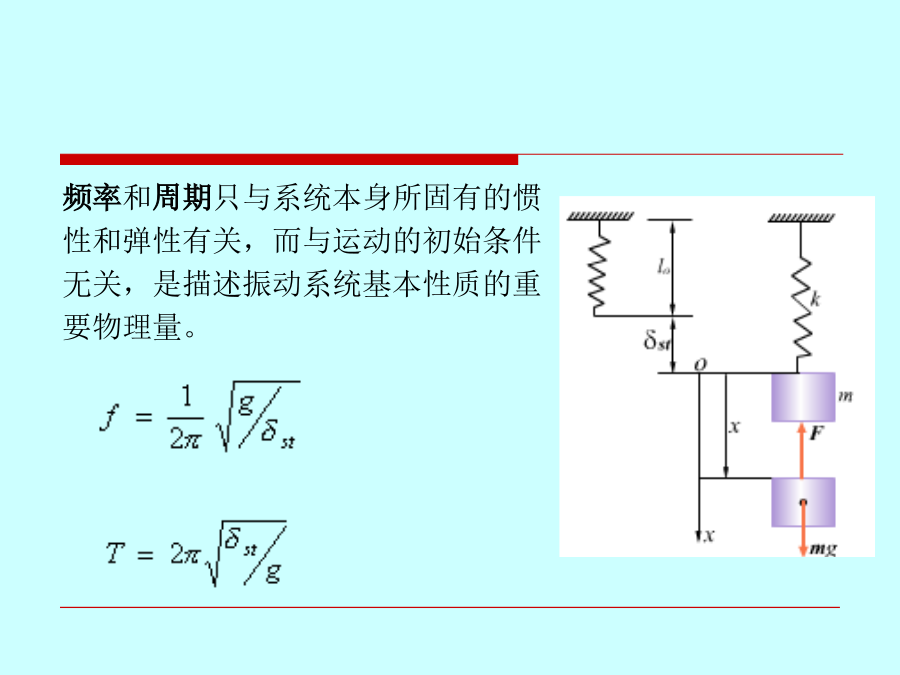
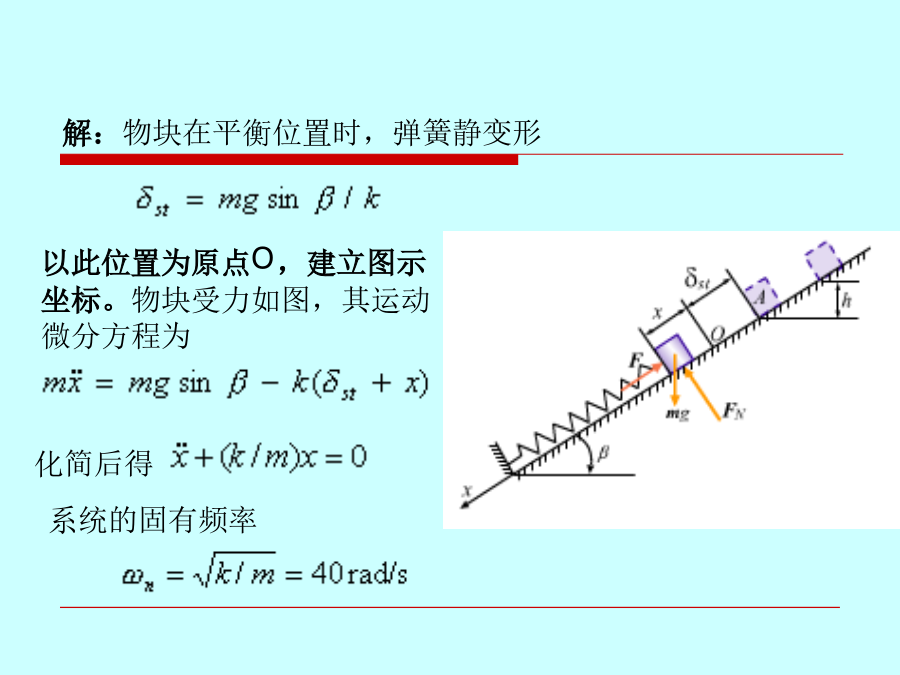
会计学系统偏离平衡位置后,仅在恢复力作用下维持的振动称为自由振动。以平衡位置为原点,建立图示坐标。物块在一般位置的受力如图示,则其振动微分方程为其通解频率和周期只与系统本身所固有的惯性和弹性有关,而与运动的初始条件无关,是描述振动系统基本性质的重要物理量。质量m=0.5kg的物块,沿光滑斜面无初速滑下,如图所示。当物块下落高度h=0.1m时撞于无质量的弹簧上并不再分离。弹簧刚度k=0.8kN/m,倾角β=300,求系统振动的固有频率和振幅,并写出物块的运动方程。解:物块在平衡位置时,弹簧静变形当物块碰上弹

振动理论基础.ppt
第十六章振动理论基础机械系统在其平衡位置附近所作的往复运动称为振动。振动现象普遍存在于自然界和工程技术中,如地震。本章仅研究单自由度系统的微振动,讨论振动的基本特征。系统偏离平衡位置后,仅在恢复力作用下维持的振动称为自由振动。以平衡位置为原点,建立图示坐标。物块在一般位置的受力如图示,则其振动微分方程为其通解频率和周期只与系统本身所固有的惯性和弹性有关,而与运动的初始条件无关,是描述振动系统基本性质的重要物理量。质量m=0.5kg的物块,沿光滑斜面无初速滑下,如图所示。当物块下落高度h=0.1m时撞于无质

振动与冲击理论基础.pptx
会计学1概述1.1机械振动1.1实际包装系统——简化1.2力学模型1.2力学模型——单自由度系统1.2力学模型——二自由度系统1.2力学模型——三自由度系统1.2力学模型——多自由度系统1.2力学模型——多自由度系统1.3机械振动的分类2单自由度线性系统的振动2.1.1无阻尼系统的自由振动(1)无阻尼系统自由振动的微分方程及求解(1)无阻尼系统自由振动的微分方程及求解(1)无阻尼系统自由振动的微分方程及求解(2)周期、频率和圆频率(2)周期、频率和圆频率之间的关系例:求质量—弹簧系统的周期、频率或圆频率。

声振动理论基础.pptx
声振动(zhèndòng)理论基础2声的振动(zhèndòng)理论基础§质点(zhìdiǎn)振动学/引言一:人耳的构造及听觉(tīngjué)特性/////声波→耳廓(收集)→外耳道→(振动)鼓膜→听小骨→耳蜗(听觉(tīngjué)收集器)→听神经→大脑听区→听觉(tīngjué)引言(yǐnyán)二:声波的振动图像进入(jìnrù)主题§质点(zhìdiǎn)振动学质点(zhìdiǎn)的自由振动固有频率(ɡùyǒupínlǜ):质点(zhìdiǎn)自由振动的一般规律:自由(zìyóu)振动的

振动与冲击理论基础.pptx
会计学1.1实际包装系统——简化1.2力学模型1.2力学模型——单自由度系统1.2力学模型——二自由度系统1.2力学模型——三自由度系统1.2力学模型——多自由度系统1.2力学模型——多自由度系统1.3机械振动的分类2单自由度线性系统的振动无阻尼系统的自由振动(1)无阻尼系统自由振动的微分方程及求解(1)无阻尼系统自由振动的微分方程及求解(1)无阻尼系统自由振动的微分方程及求解(2)周期、频率和圆频率(2)周期、频率和圆频率之间的关系例:求质量—弹簧系统的周期、频率或圆频率。(3)计算固有频率的能量法(3
