
解释结构模型ISM及其应用PPT课件.pptx

天马****23







亲,该文档总共30页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

解释结构模型ISM及其应用ppt课件.pptx
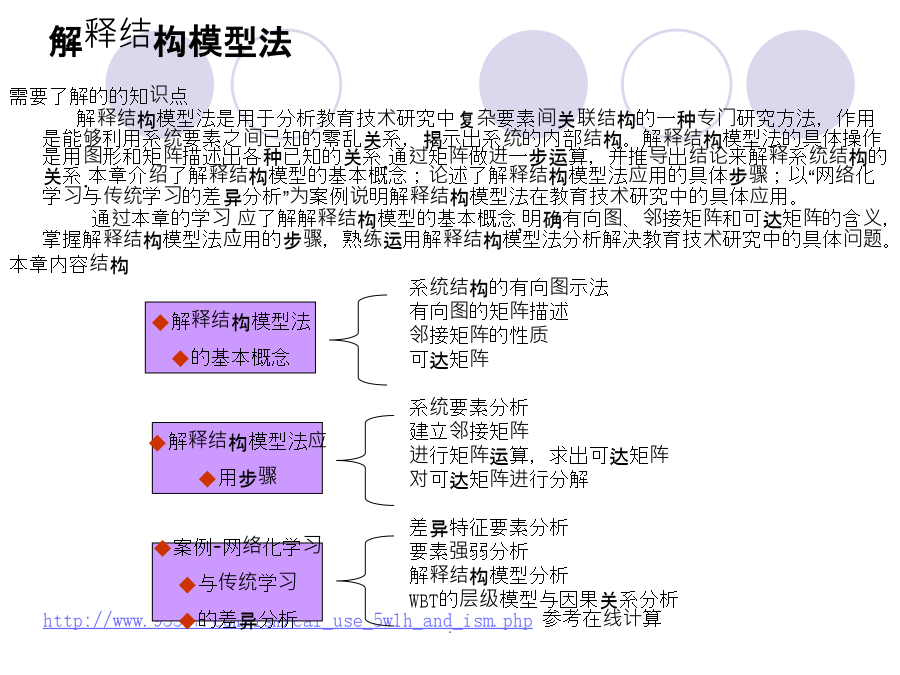
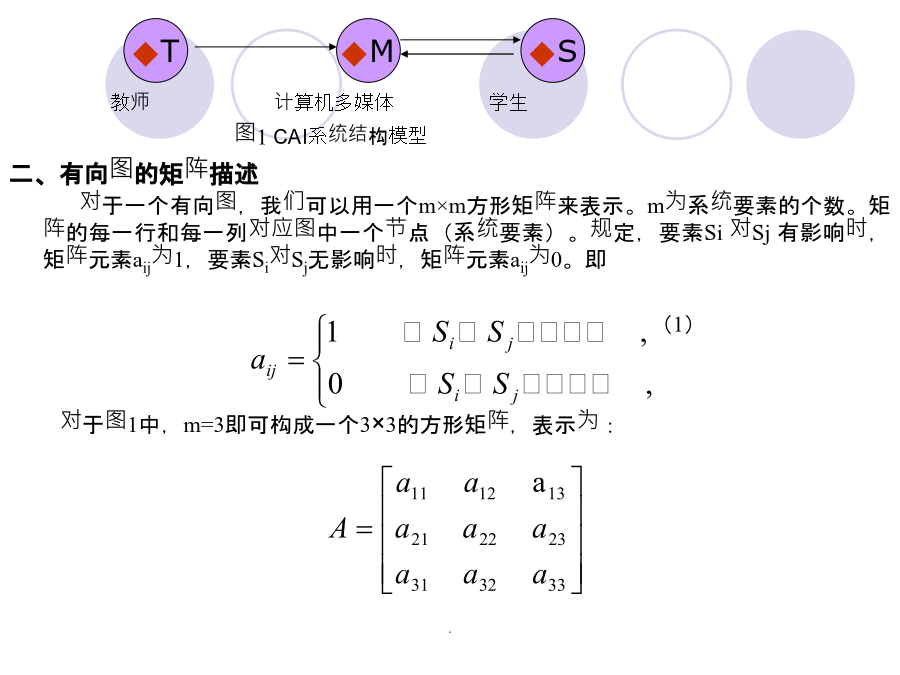
12345解释结构模型法第一节解释结构模型法的基本概念定义:解释结构模型法(InterpretativeStructuralModellingMethod,简称ISM方法)ISM方法是现代系统工程中广泛应用的一种分析方法,它在揭示系统结构,一、系统结构的有向图示法有向图形——是系统中各要素之间的联系情况的一种模型化描述方法。它由节点和边两部分组成节点——利用一个圆圈代表系统中的一个要素,圆圈标有该要素的符号;边——用带有箭头的线段表示要素之间的影响。箭头代表影响的方向。教师计算机多媒体学生图1CAI系统结

解释结构模型ISM及其应用PPT课件.pptx
12345解释结构模型法第一节解释结构模型法的基本概念定义:解释结构模型法(InterpretativeStructuralModellingMethod,简称ISM方法)ISM方法是现代系统工程中广泛应用的一种分析方法,它在揭示系统结构,一、系统结构的有向图示法有向图形——是系统中各要素之间的联系情况的一种模型化描述方法。它由节点和边两部分组成节点——利用一个圆圈代表系统中的一个要素,圆圈标有该要素的符号;边——用带有箭头的线段表示要素之间的影响。箭头代表影响的方向。教师计算机多媒体学生图1CAI系统结

解释结构模型ISM及其应用.ppt
12345解释结构模型法第一节解释结构模型法的基本概念定义:解释结构模型法(InterpretativeStructuralModellingMethod,简称ISM方法)ISM方法是现代系统工程中广泛应用的一种分析方法,它在揭示系统结构,一、系统结构的有向图示法有向图形——是系统中各要素之间的联系情况的一种模型化描述方法。它由节点和边两部分组成节点——利用一个圆圈代表系统中的一个要素,圆圈标有该要素的符号;边——用带有箭头的线段表示要素之间的影响。箭头代表影响的方向。教师计算机多媒体学生图1CAI系统结

第二讲解释结构模型及其应用ppt课件.ppt
经济管理数学I第二讲解释结构模型ISM及其应用21解释性结构建模方法结构模型:系统有很多要素构成,建立要素之间的相互关系,即系统的结构模型,是系统分析的重要方法。1、微积分12、工程制图初步3、算法语言4、英语5、体育6、中国革命史通论27、体育28、军事理论9、普物实验110、体育311、当代资本主义12、普通物理实验113、电路原理114、工程数学15、数字电子技术基础16、体育417、普通物理实验218、工程基础19、体育520、电机与电力拖动基础21、模拟电子基础22、计算机原理及应用123、电子

解释结构模型(ISM)在教学计划制定中的应用.pdf
http://www.paper.edu.cn解释结构模型(ISM)在教学计划制定中的应用戴敏利1,2,陆峰1,2,李敏11、华中师范大学教育信息技术工程研究中心,2、华中师范大学信息技术系,湖北武汉430079摘要:随着高等教育事业的发展和社会对人才需求的不断变化,专业设置在不断的更新和完善,各专业的课程设置也随之不断调整,由此给课程计划的制定带来很大的困难。本文着重讨论了在高校教学计划制定的过程中,有效运用解释结构模型(ISM),分析各专业课程之间的逻辑关系,构建课程计划图以对课程体系结构进行统一规划
