柯西积分公式及高阶导数公式课程-豆柴文库

柯西积分公式及高阶导数公式课程.pptx

2024-10-11

20金币

730KB

28页

快乐****蜜蜂

实名认证

内容提供者

1/10

2/10

3/10

4/10

5/10

6/10

7/10

8/10

9/10

10/10

亲，该文档总共28页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

相关资料

柯西积分公式及高阶导数公式课程.pptx

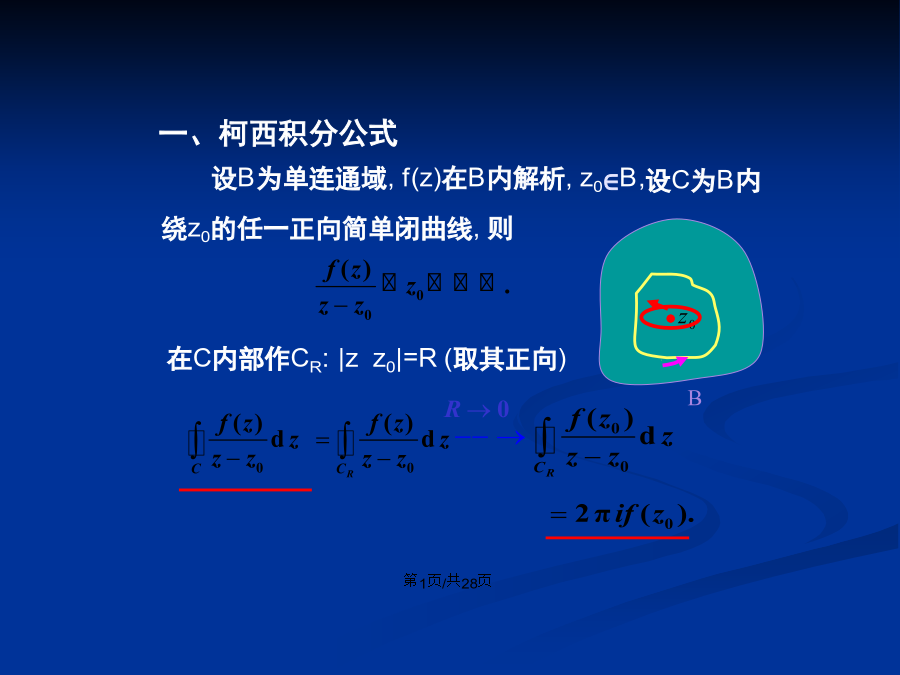
会计学设B为单连通域,f(z)在B内解析,z0∈B,定理(柯西积分公式)：如果f(z)在区域D内处处解析,C为D内的任何一条正向简单闭曲线,它的内部完全含于D,z0为C内部的任一点,则证明:由于f(z)在z0连续,——柯西积分公式特别,如C:|z-z0|=R,z=z0+Reiq,则上式成为例1：求下列积分(沿圆周正方向)的值:如果各阶导数存在,并且导数运算可在积分号下说明:证明首先考虑n=1的情形.因为z0在C的内部,利用类似的方法可求得例1.求积分例2.求积分例3.求积分于是柯西-古萨(Cauchy－G

2024-10-11

730KB

【中学课件】3-3柯西积分公式和解析函数的高阶导数.ppt

12345678910111213141516171819202122232425262728293031323334353637383940414243

2023-12-11

1.1MB

33柯西积分公式.ppt

第三节柯西积分公式一、解析函数的柯西积分公式2.柯西积分公式定理3.3.1(柯西积分公式)例1例1由柯西积分公式例2例2例2例2例2例3例3二、解析函数的任意阶可导性和莫勒拉定理定理3.3.2根据导数的定义,根据导数的定义,根据导数的定义,推论3.3.1例4例4例4例5例6例6定理3.3.3(莫勒拉(Morera)定理)定理3.3.3(莫勒拉(Morera)定理)三、柯西不等式与刘维尔定理三、柯西不等式与刘维尔定理2.柯西不等式证证3.刘维尔定理3.刘维尔定理例7例8四、调和函数四、调和函数四、调和函数2

2024-10-18

2.4MB

柯西积分公式及高阶导数公式市公开课一等奖省赛课获奖PPT课件.pptx

第三章复变函数积分设B为单连通域,f(z)在B内解析,z0∈B,定理(柯西积分公式)：假如f(z)在区域D内处处解析,C为D内任何一条正向简单闭曲线,它内部完全含于D,z0为C内部任一点,则证实:因为f(z)在z0连续,——柯西积分公式尤其,如C:|z-z0|=R,z=z0+Reiq,则上式成为例1：求以下积分(沿圆周正方向)值:假如各阶导数存在,而且导数运算可在积分号下说明:证实首先考虑n=1情形.因为z0在C内部,于是存在M>0,使得|f(z)|M.又因为z0是C利用类似方法可求得例1.求积分例2.

2024-10-28

1.8MB

【中学课件】3-3Cauchy积分公式和高阶导数公式.ppt

1.问题的提出2.Cauchy积分公式证明：以为心作一完全包含于内的圆盘并且记其边界为圆。在上挖去圆盘余下的点集是一个闭区域。在上函数解析由柯西定理有：在这里沿的纠纷是按照区域的正向取的沿的积分是按正向取的即逆时针方向。以下我们证明：定理1对于由条围线所围成的复连通区域仍然有效．（如教材66页定理1那样构成）例1例2关于Cauchy积

2023-12-11

3.7MB