
信号与线性系统分析总结.docx

92****sc










亲,该文档总共34页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

信号与线性系统分析总结.docx
信号与线性系统分析总结1.信号概述信号是描述物理现象、系统状态和过程变化的数学表示。在信号与线性系统分析中,信号可以分为连续时间信号和离散时间信号。连续时间信号是指在时间上可以无限分割的信号,其函数形式为f(t)Acos(t+),其中A表示幅度,表示角频率,t表示时间,表示相位。离散时间信号是指在时间上有限个采样点的信号,其函数形式为x[n]Acos(n+),其中A表示幅度,表示角频率,n表示采样点序号,表示相位。信号的分类主要包括周期信号、非周期信号、正弦波信号、余弦波信号等。周期信号是指具有固定周期的

《信号及线性系统分析》.ppt
信号与线性系统分析绪论第一章信号与系统第二章连续系统的时域分析第三章离散系统的时域分析第四章连续系统的频域分析第五章连续系统的s域分析第六章离散时间系统的z域分析第七章系统函数第八章系统的状态变量分析绪论它是通信及信号专业的必修课程、“电路理论”课程的继续、深入和发展,用数学工具分析物理概念。实际上它分为信号分析和系统分析两部分:研究在给定系统结构的条件下,求得系统功能及输出特性的一般方法。信号与系统紧密相联不可分割,分析信号是目的,分析系统是手段,两者缺一不可。设置本课程的原因信号要由不同的系统来产生、

信号与线性系统分析.docx
信号与线性系统分析一、概要《信号与线性系统分析》是一篇深入剖析信号与线性系统之间关系的文章。本文将探讨信号的基本概念,包括其定义、分类和表现方式,并进一步分析线性系统的特性和行为。文章旨在为读者提供一个全面的视角,理解信号在各类系统中的传输和处理方式,以及线性系统如何响应这些信号。全文将通过理论和实例的结合,帮助读者更好地理解和应用信号与线性系统的相关知识。该文章也将涉及在实际工程、通信和科学研究领域中对信号与系统分析的重要性和应用前景。在阅读本文之后,读者将能够更深入地理解信号与线性系统的基本概念,以及

信号与线性系统分析.ppt
第1章绪论误差定义及表达形式测量误差来源的分析测量误差按误差性质的分类处理有效数字定义及选取门捷列夫(1834-1907)我常说的一句话是:钱学森王大珩等第一节研究误差的意义第二节误差的基本概念误差(Error):约定真值(ConventionalTrueValue)误差绝对误差(AbsoluteError)修正值(Correction)【例1-1】定义绝对误差和相对误差的比较引用误差(FiducialErrorofaMeasuringInstrument)我国电工仪表、压力表的准确度等级(Accurac
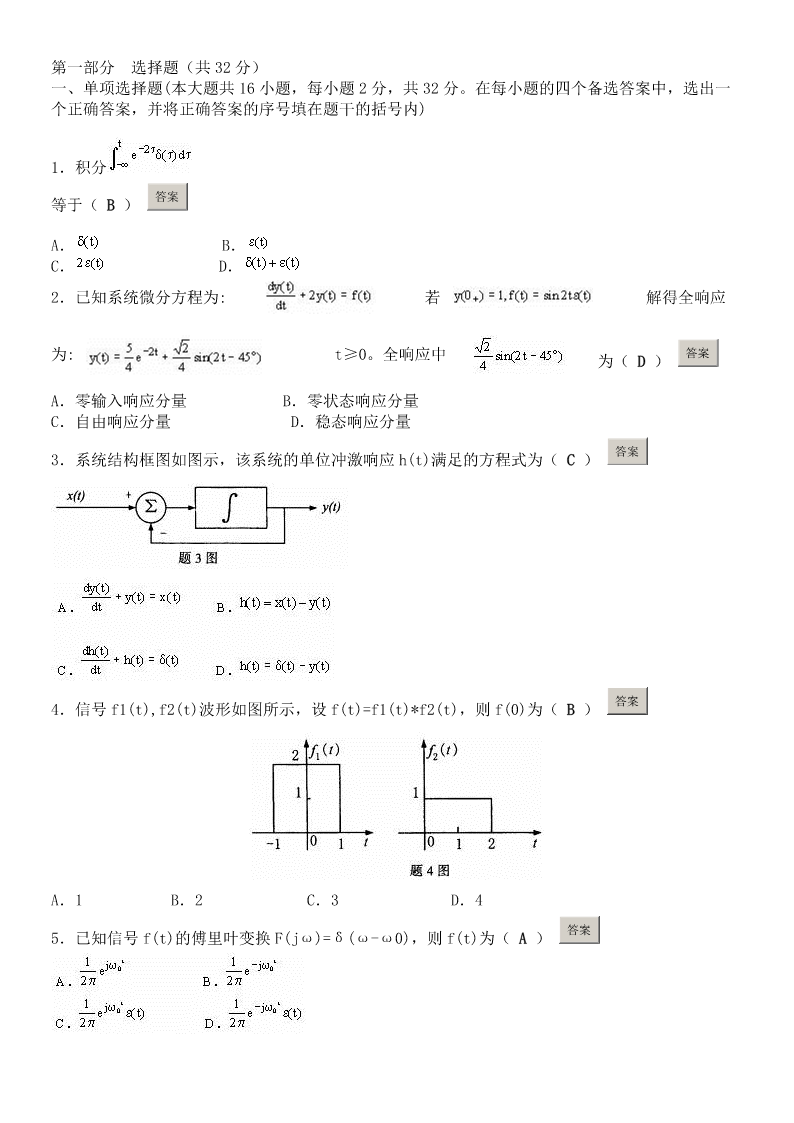
信号与线性系统分析试卷.pdf
第一部分选择题(共32分)一、单项选择题(本大题共16小题,每小题2分,共32分。在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内)1.积分答案等于(B)A.B.C.D.2.已知系统微分方程为:若解得全响应答案为:t≥0。全响应中为(D)A.零输入响应分量B.零状态响应分量C.自由响应分量D.稳态响应分量答案3.系统结构框图如图示,该系统的单位冲激响应h(t)满足的方程式为(C)答案4.信号f1(t),f2(t)波形如图所示,设f(t)=f1(t)*f2(t),则f(0)为(
