
第7章一阶电路和二阶电路的时域分析.ppt

15****92





亲,该文档总共109页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

一阶电路和二阶电路的时域分析.doc
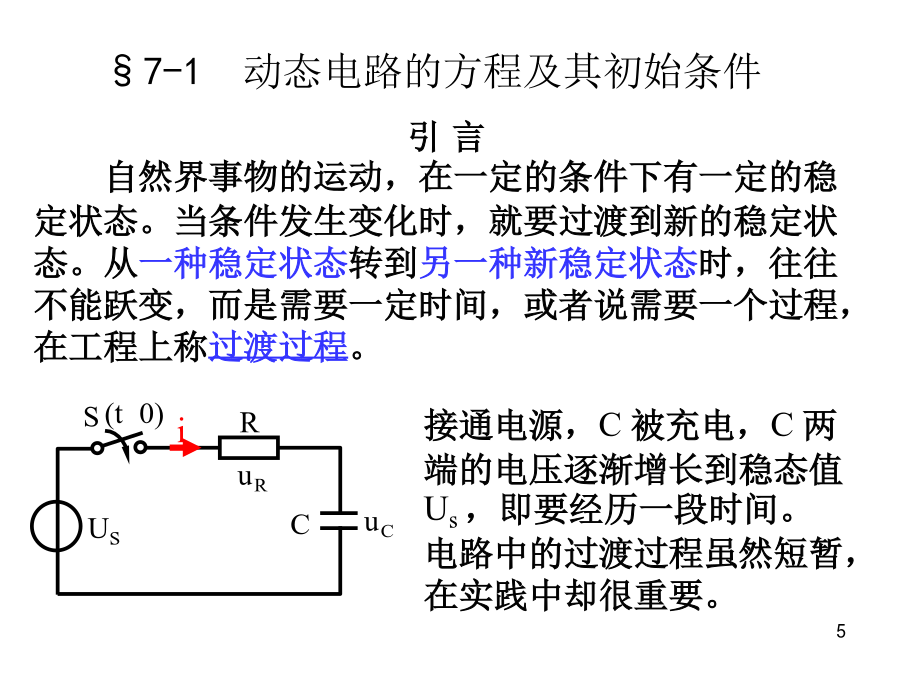
Chapter7一阶电路和二阶电路的时域分析Chapter7一阶电路和二阶电路的时域分析主要内容1.动态电路的方程及其初始条件;2.一阶和二阶电路的零输入响应、零状态响应和全响应的概念及求解;3.一阶和二阶电路的阶跃响应概念及求解。§7-1动态电路的方程及其初始条件一、动态电路的方程1.动态电路:含有动态元件(电容或电感)的电路。2.动态电路的方程:电路中有储能元件(电容或电感)时,因这些元件的电压和电流的约束关系是通过导数(或积分)表达的。根据KCL、KVL和支路方程式

第7章一阶电路和二阶电路的时域分析.ppt
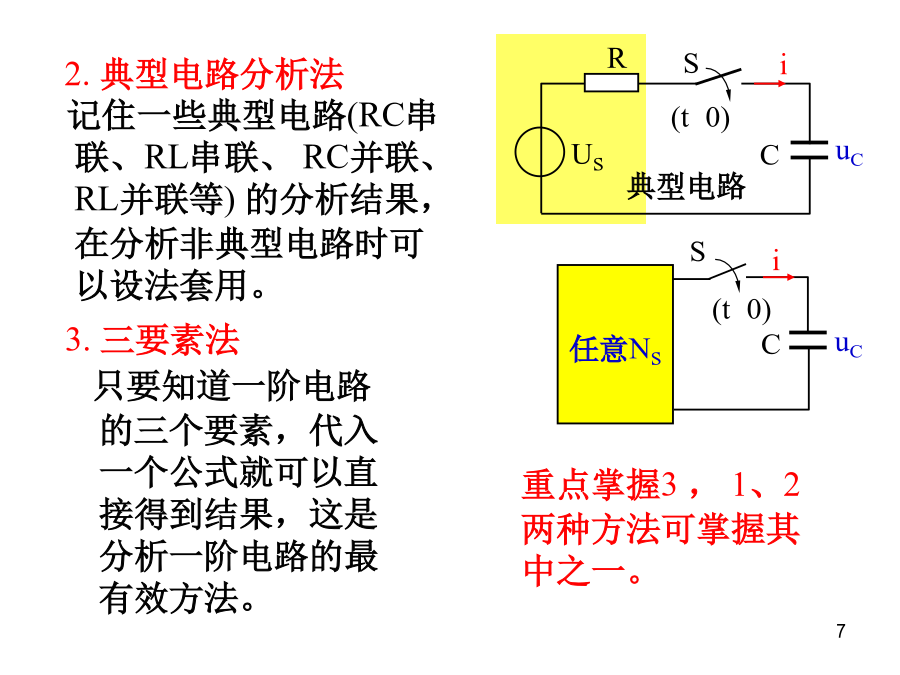
第七章一阶电路和二阶电路的时域分析§7―1动态电路的议程及其初始条件§7―2一阶电路的零输入响应§7―3一阶电路的零状态响应§7―4一阶电路的全响应§7―5二阶电路的零输入响应§7―6二阶电路的零状态响应和全响应§7―7一阶电路和二阶电路的阶跃响应§7―8一阶电路和二阶电路的冲激响应*§7―9卷积积分*§7―10状态方程*§7―11动态电路时域分析中的几个问题1.换路定则和电路初始值的求法;2.掌握一阶电路的零输入响应、零状态响应、全响应的概念和物理意义;3.会计算和分析一阶动态电路(重点是三要素法);4

第7章-一阶电路和二阶电路的时域分析.ppt
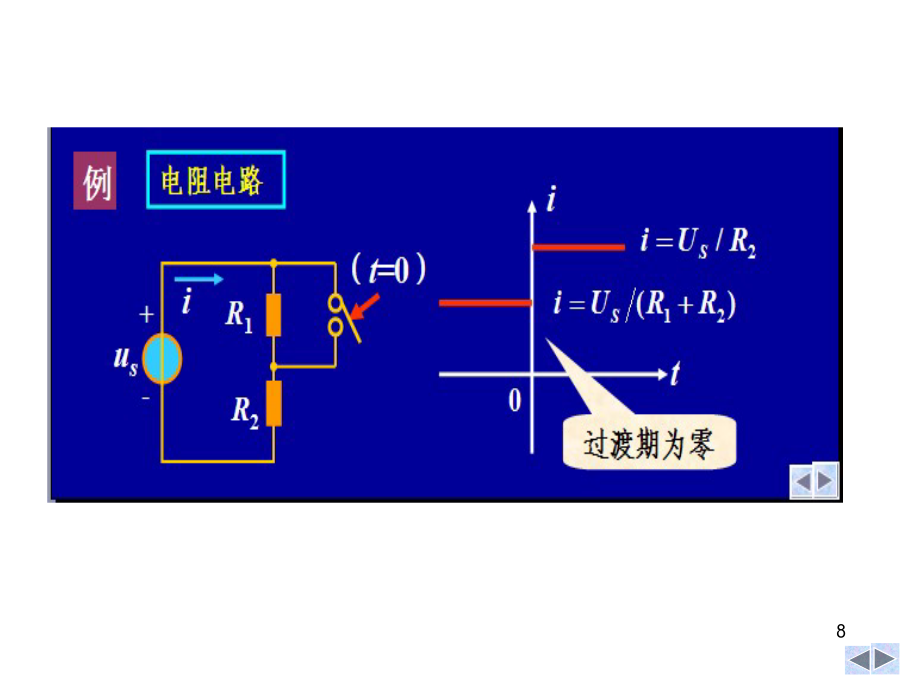
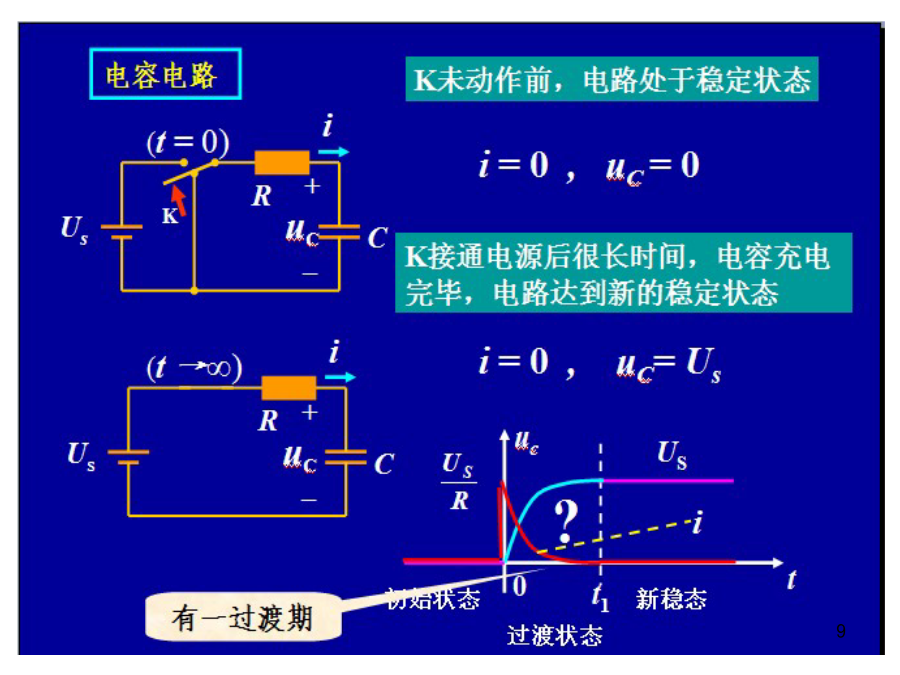
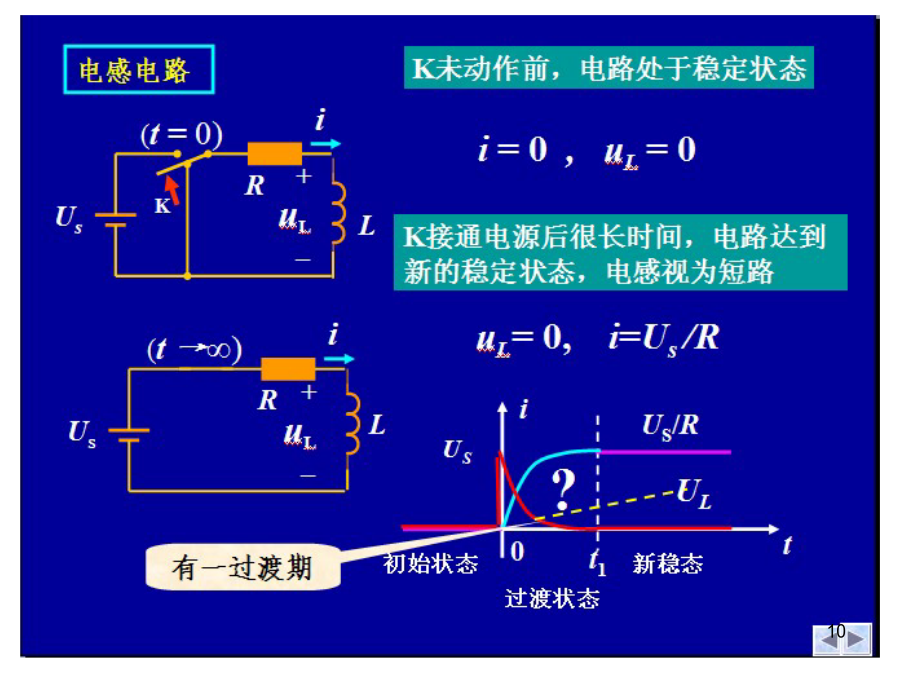
动态电路的方程及其初始条件一阶电路的零输入响应、零状态响应和全响应的概念及求解;含有动态元件电容和电感的电路称动态电路。例i=0,uC=UsuL=0,i=Us/R下页过渡过程产生的原因应用KVL和电容的VCR得:应用KVL和电感的VCR得:有源电阻电路二阶电路一阶电路高阶电路复频域分析法稳态分析和动态分析的区别t=0+与t=0-的概念图示为电容放电电路,电容原先带有电压Uo,求开关闭合后电容电压随时间的变化。t=0+时刻q(0+)=q(0-)电感的初始条件L(0+)=L(0-)L(0+)=L(0-

电路件一阶电路和二阶电路时域分析.pptx
会计学02十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月202402十月

第7章-一阶电路和二阶电路的时域分析.ppt
动态电路的方程及其初始条件一阶电路的零输入响应、零状态响应和全响应的概念及求解;含有动态元件电容和电感的电路称动态电路。例i=0,uC=UsuL=0,i=Us/R下页过渡过程产生的原因应用KVL和电容的VCR得:应用KVL和电感的VCR得:有源电阻电路二阶电路一阶电路高阶电路复频域分析法稳态分析和动态分析的区别t=0+与t=0-的概念图示为电容放电电路,电容原先带有电压Uo,求开关闭合后电容电压随时间的变化。t=0+时刻q(0+)=q(0-)电感的初始条件L(0+)=L(0-)L(0+)=L(0-
