
第八章2应力应变状态分析.ppt

你的****书屋








亲,该文档总共85页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

第八章2应力应变状态分析.ppt
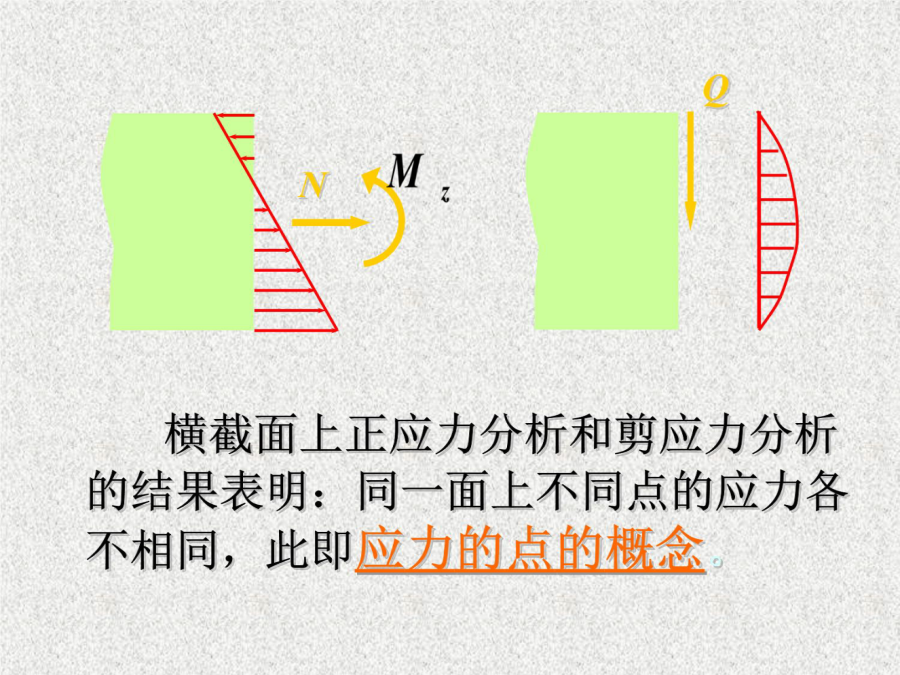
第九章应力状态分析与强度理论第九章应力状态分析和强度理论§9–1应力状态的概念四、普遍状态下的应力表示应力的三个重要概念过一点不同方向面上应力的集合,称之为这一点的应力状态(StateoftheStressesofaGivenPoint)。3、一点应力状态的描述y(PlaneStateofStresses)x三向应力状态应力状态的概念由平衡即可确定任意方向面上的正应力和切应力。5示例二xyxtzx七、主单元体、主面、主应力:单向应力状态(UnidirectionalStateofStress):一个主应

第八章应力、应变状态分析.ppt
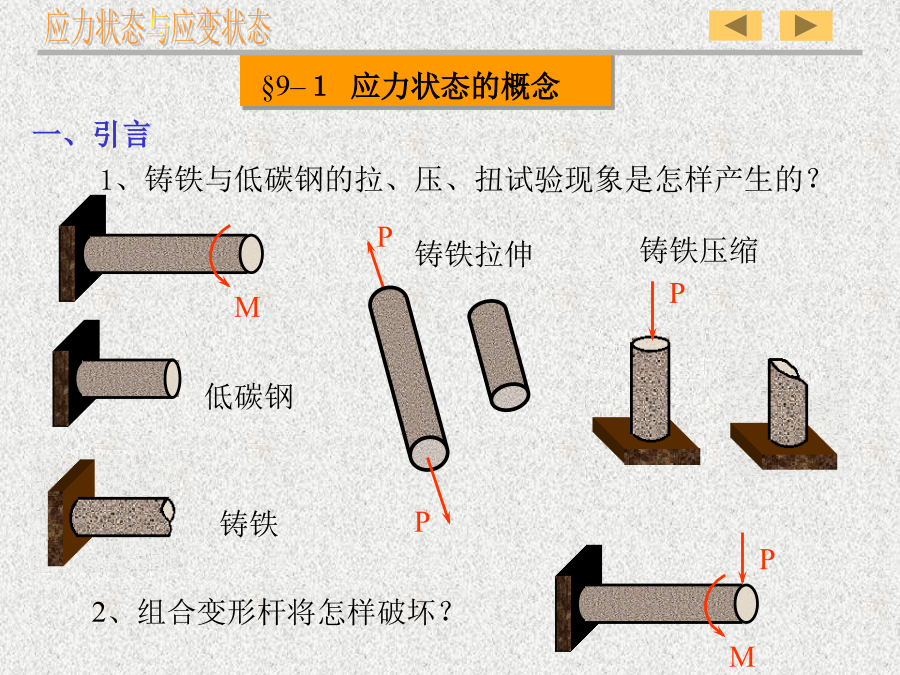
第七章应力与应变状态分析第八章应力与应变状态分析§8—1应力状态概述组合变形杆将怎样破坏?通过轴向拉伸杆件内点不同(方向)截面上的应力情况(集合)。)F30xyb平面应力状态:单向应力状态和二向应力状态的总称。§8-2平面应力状态分析——解析法s考虑切应力互等和三角变换,得:符号规定:、“”正负号同“”;、“ta”正负号同“t”;、“a”为斜面的外法线与Χ轴正向的夹角,由Χ轴逆时针转到斜面为正,顺时针为负。——主平面的位置2、τ的极值及所在平面t例:如图所示单元体,求α斜面的应力及主应力、主平

第八章应力、应变状态分析.ppt
第七章应力与应变状态分析第八章应力与应变状态分析§8—1应力状态概述组合变形杆将怎样破坏?通过轴向拉伸杆件内点不同(方向)截面上的应力情况(集合)。)F30xyb平面应力状态:单向应力状态和二向应力状态的总称。§8-2平面应力状态分析——解析法s考虑切应力互等和三角变换,得:符号规定:、“”正负号同“”;、“ta”正负号同“t”;、“a”为斜面的外法线与Χ轴正向的夹角,由Χ轴逆时针转到斜面为正,顺时针为负。——主平面的位置2、τ的极值及所在平面t例:如图所示单元体,求α斜面的应力及主应力、主平

第八章3应力应变状态分析.ppt
第八章应力应变状态分析一.研究应力状态的意义二、一点的应力状态x(1)应力分量的角标规定:第一角标表示应力作用面,第二角标表示应力平行的轴,两角标相同时,只用一个角标表示。低碳钢、铸铁试件受扭时的破坏现象。CL10TU2主平面§8-2平面应力状态下的应力分析二.应力分析的解析法σ:拉应力为正τ:顺时针转动为正α:逆时针转动为正平衡对象——用斜截面截取的微元局部-注:三角公式讨论:§8-3.主应力由于该面上午切应力,所以他们就是最大主应力和最小主应力。由由:§8-4应力分析的图解法—应力圆1.莫尔(Mo

应力与应变状态分析学习教案.ppt
会计学234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071内容(nèiróng)总结
