应力状态理论与强理论.pptx

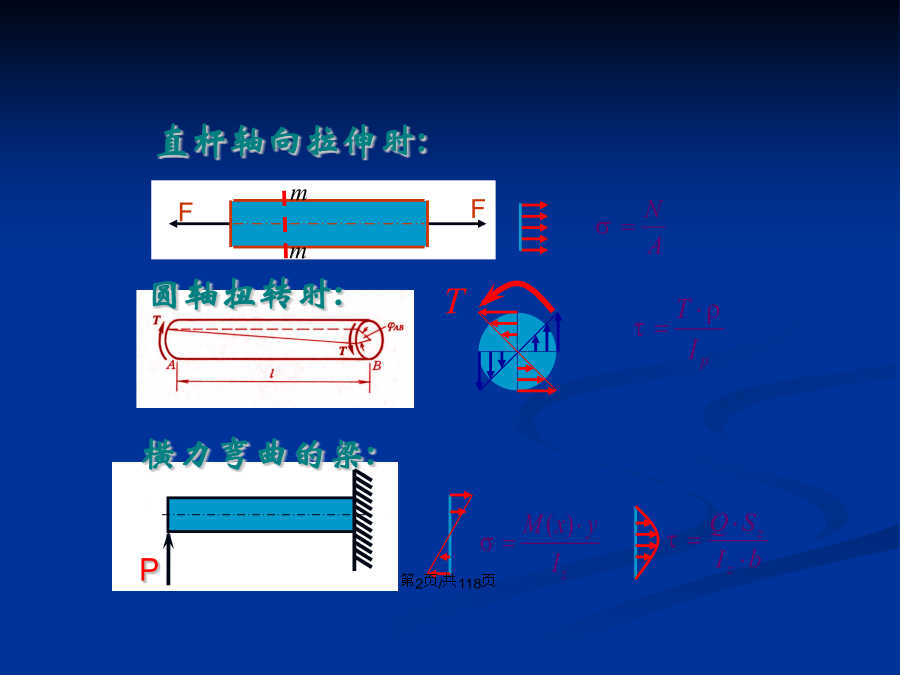
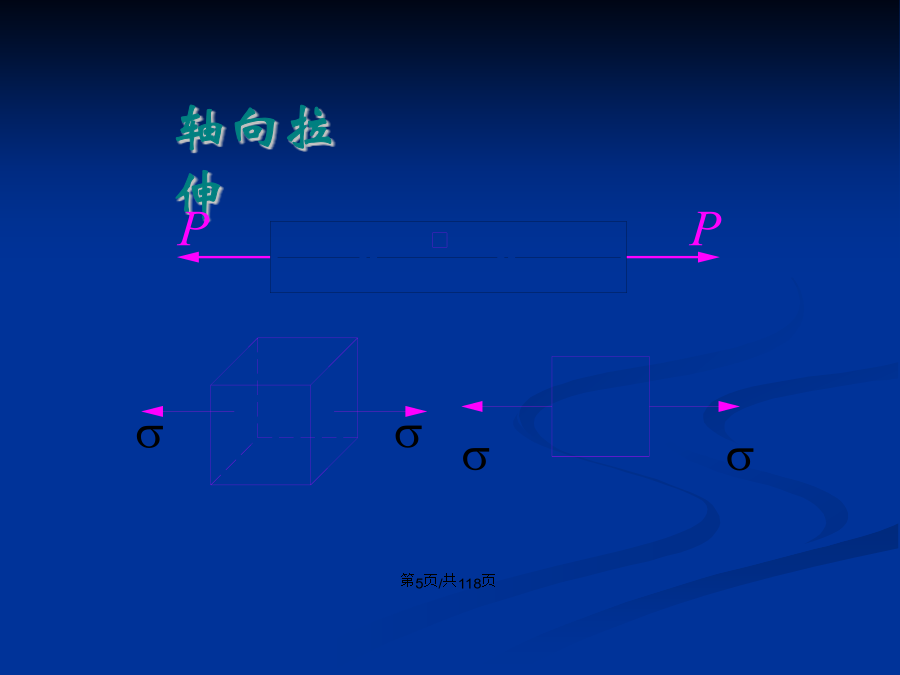
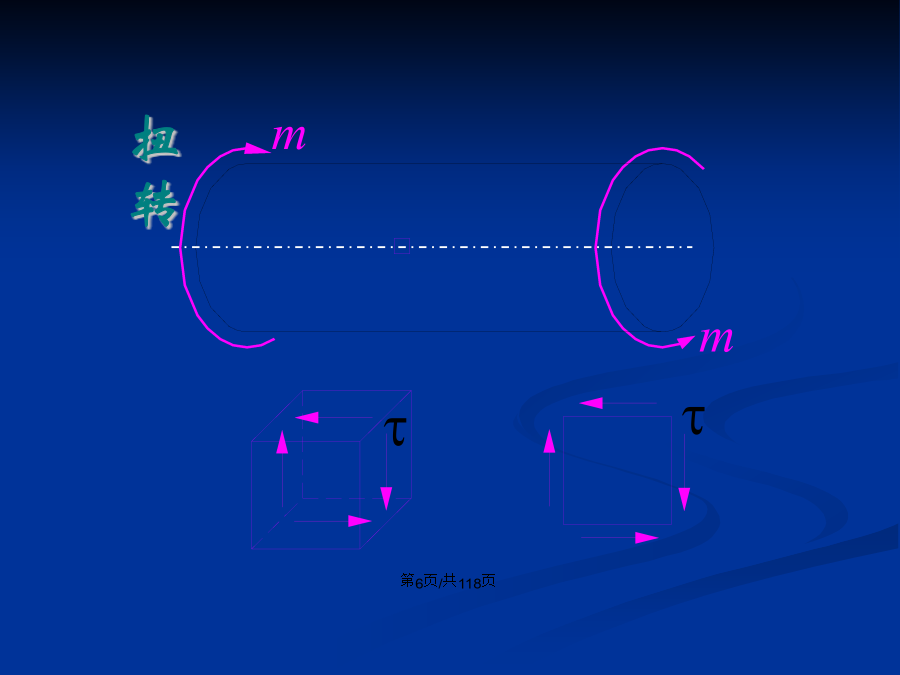
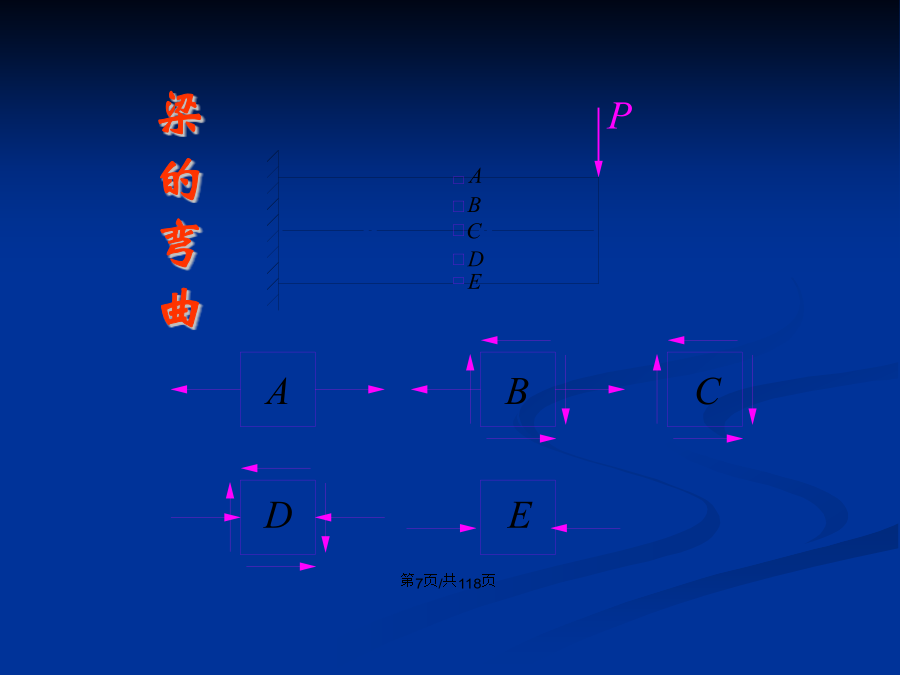
会计学铸铁直杆轴向拉伸时:§7-1应力状态的概念轴向拉伸扭转梁的弯曲主平面（pincipalplane)：剪应力为零的平面主应力(pincipalstress)：主平面上的正应力主方向(pincipaldirections)：主平面的法线方向应力状态的分类实例一实例三实例四按工程应用传统观念，判断构件强度取决于危险点的应力状态。
危险点是怎样达到破坏的呢？
在什么方向最容易破坏呢？
以下将从一点处应力状态分析中，找出哪个截面上有正应力极值，哪个截面上有剪应力极值，以此作出构件强度的判据。§7-2平面应力状态分析一、斜截面上的应力—解析法：拉应力为正
τ:顺时针转动为正
：逆时针转动为正平衡原理的应用——微元局部的平衡方程-注：三角公式讨论：斜截面上的应力公式斜截面上的正应力取极值条件极值正应力：二、斜截面上的应力—图解法应力圆莫尔(Mohr)圆根据已知单元体上的应力x、y、τx画应力圆利用应力圆求任意斜截面上的应力三种对应关系点面对应转向对应、二倍角对应应力圆的画法应力圆的应用——信息源例1、请您用解析法与图解法求图示单元体(1)指定斜截面上的正应力和剪应力; (2)主应力值及主方向，并画在单元体上；(3)极值剪应力值。解：(一)解析法:x、y平面剪应力共同所指象限为正应力极大值所在象限/(二)图解法:
作应力圆，从应力圆上可量出：例2、讨论圆轴扭转时的应力状态，并分析低碳钢、铸铁试件受扭时的破坏现象。低碳钢/§7-3空间应力状态分析首先分析平行于主应力之一（例如3）的各斜截面上的应力。/同理，在平行于2的各个斜截面上，其应力对应于由主应力1和3所画的应力圆圆周上各点的坐标。/在平行于1的各个斜截面上，其应力对应于由主应力2和3所画的应力圆圆周上各点的坐标。/这样，单元体上与主应力之一平行的各个斜截面上的正应力和剪应力，可由三个应力圆圆周上各点的坐标来表示。与三个主方向都不平行的任意斜截面，弹性力学中已证明，其应力n和τn可由图中阴影面内某点的坐标来表示。在三向应力状态情况下：例4、单元体各面上的应力如图所示，试求主应力值和最大切应力值。例5、求图示应力状态的主应力和最大剪应力（应力单位为MPa）。解：例6、求图示应力状态的主应力和最大剪应力（应力单位MPa）。纯剪切应力状态:练习1：求图示应力状态的主应力和最大剪应力（应力单位为MPa）。解：§7-4广义胡克定律：横向变形系数
（泊松比）/广义胡克定律对于二向应力状态：例7、图示一边长为a=200mm的正方体混凝土块，无空隙地放在刚性凹座内，上表面受压力P=300kN的作用，已知混凝土的泊松比=1/6，试求凹座壁上所受的压力。由受力的对称性知例8、图示矩形截面拉杆，截面宽为b，高h，材料的弹性常数E、已知。在拉杆表面的图示位置有直角ABC，试求杆受拉力F后线段BC以及直角ABC的改变量。BC段的伸长量为：§7-5空间应力状态下的比能一般情况下，单元体将同时发生体积改变和形状改变。因此，应变能密度可相应分成两部分：体积改变能密度和畸变能密度。§7-6强度理论铸铁和低碳钢的扭转破坏说明：
相同的受力方式，材料不同破坏方式不同。在复杂应力状态下，材料破坏不仅与各个主应力（含大小和方向）有关，而且和它们之间的比值也有关，不同的主应力组合，对应不同的破坏应力，为此，必须测出在不同主应力比值下的破坏应力，实际上，工程中的受力构件其主应力组合有无限多种，无法一一进行实验。到目前为止，实现复杂应力状态的试验机及测试手段仅有有限的几种，对于众多的主应力组合，在技术上难以实现。当危险点处于简单应力状态时的强度条件无论是简单或复杂应力状态，引起失效的因素是相同的。二、常用的四种强度理论1、最大拉应力理论（第一强度理论）试验证明，这一理论与铸铁、岩石、砼、陶瓷、玻璃等脆性材料的拉断试验结果相符，这些材料在轴向拉伸时的断裂破坏发生于拉应力最大的横截面上。脆性材料的扭转破坏，也是沿拉应力最大的斜面发生断裂，这些都与最大拉应力理论相符，但这个理论没有考虑其它两个主应力的影响。2、最大伸长线应变理论（第二强度理论）由此导出失效条件的应力表达式为：煤、石料或砼等材料在轴向压缩试验时，如端部无摩擦，试件将沿垂直于压力的方向发生断裂，这一方向就是最大伸长线应变的方向，这与第二强度理论的结果相近。(二)、关于屈服的强度理论用应力表示的屈服破坏条件：第三强度理论曾被许多塑性材料的试验结果所证实，且稍偏于安全。这个理论所提供的计算式比较简单，故它在工程设计中得到了广泛的应用。该理论没有考虑中间主应力σ2的影响，其带来的最大误差不超过15％，而在大多数情况下远比此为小。2、形状改变能密度理论(第四强度理论)（畸变能密度）单向拉伸时：这个理论和许多塑性材料的试验结果相符，用这个理论判断碳素钢