
二次函数y=ax2 k的图象和性质 (2).docx

yy****24



在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

《二次函数y=ax2 k的图象和性质》.1.3二次函数y=ax2 k图象性质》课件.pptx
22.1.3二次函数的图像和性质22、二次函数y=2x2的图象是____,它的开口向___,顶点坐标是____;对称轴是____,在对称轴的左侧,y随x的增大而______,在对称轴的右侧,y随x的增大而______,函数y=2x2当x=______时,y有最______值,其最______值是______。猜想:二次函数y=x2-2与y=x2的图象的关系:_____________________________________________得到.-5抛物线y=x2、y=x2+1、y=x2-1的形状、
二次函数y=ax 2 k的图象与性质.1.3二次函数y=ax2 k的图象和性质.ppt
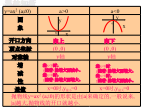
温故知新试一试:x二次函数的图像x二次函数的图象y=-x2-2函数y=ax2(a≠0)和函数y=ax2+k(a≠0)的图象形状,只是位置不同;当k>0时,函数y=ax2+k的图象可由y=ax2的图象向平移个单位得到,当k<0时,函数y=ax2+k的图象可由y=ax2的图象向平移个单位得到。(1)函数y=4x2+5的图象可由y=4x2的图象向平移个单位得到;函数y=4x2-11的图象可由y=4x2的图象向平移个单位得到.二次函数的图象课堂小结课后作业例题讲解y=ax2+ky=ax2+k课后作业

二次函数y=ax2 k的图象和性质.ppt
22.1.3二次函数y=ax2+k的图像与性质学习目标自学指导检测一(5分钟)函数y=ax2(a≠0)和函数y=ax2+k(a≠0)的图象形状,只是位置____;当k>0时,函数y=ax2+k的图象可由y=ax2的图象向平移个单位得到,当k<0时,函数y=ax2+k的图象可由y=ax2的图象向平移______个单位得到。1.抛物线y=-3x2平移后得到抛物线y=ax2-7,则a=____.y=ax2+ky=ax2+k检测三:作业:1、必做题:见作业设计2、选做题:见作业设计

二次函数y=ax2 k的图象和性质.docx
22.1.3二次函数y=a(x-h)2+k的图象和性质第1课时二次函数y=ax2+k的图象和性质教学目标:1.会用描点法画出y=ax2+k的图象.2.掌握形如y=ax2+k的二次函数图象的性质,并会应用.3.理解二次函数y=ax2+k与y=ax2之间的联系.重点难点:会用描点法画出二次函数y=ax2+b的图象是教学的难点。掌握二次函数y=ax2+b的性质,理解函数y=ax2+b与函数y=ax2的相互关系是教学重点。教学过程:一、复习引入1.我们主要学习了二次函数y=ax2哪些性质开口,顶点坐标,对称轴,增

二次函数y=ax2 k的图象和性质 (2).docx
教学目标1.知识与能力能够作出函数y=ax2+k的图象,并能够理解函数y=ax2+k与y=ax2之间的关系,理解a、k对二次函数图象的影响;能够正确说出函数图象的开口方向、对称轴和顶点坐标。2.过程与方法通过学生自己的探索活动,对二次函数性质的研究,达到对抛物线自身的特点的认识和对二次函数性质的理解;经历探索二次函数的图象的作法和性质的过程,培养学生的探索能力。3.情感态度与价值观通过动手操作,激发学生的学习兴趣,在互动中让学生学会和他人合作、交流,同时让学生在猜想与探究中,体验学习的快乐。教材分析二次函
