特殊平行四边形性质与判定运用复习.pptx

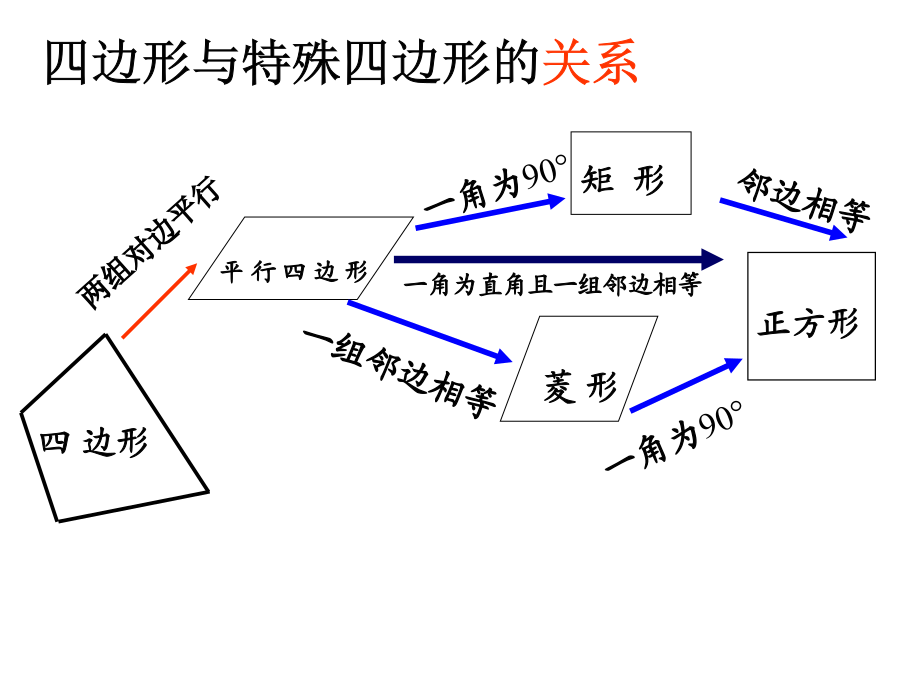
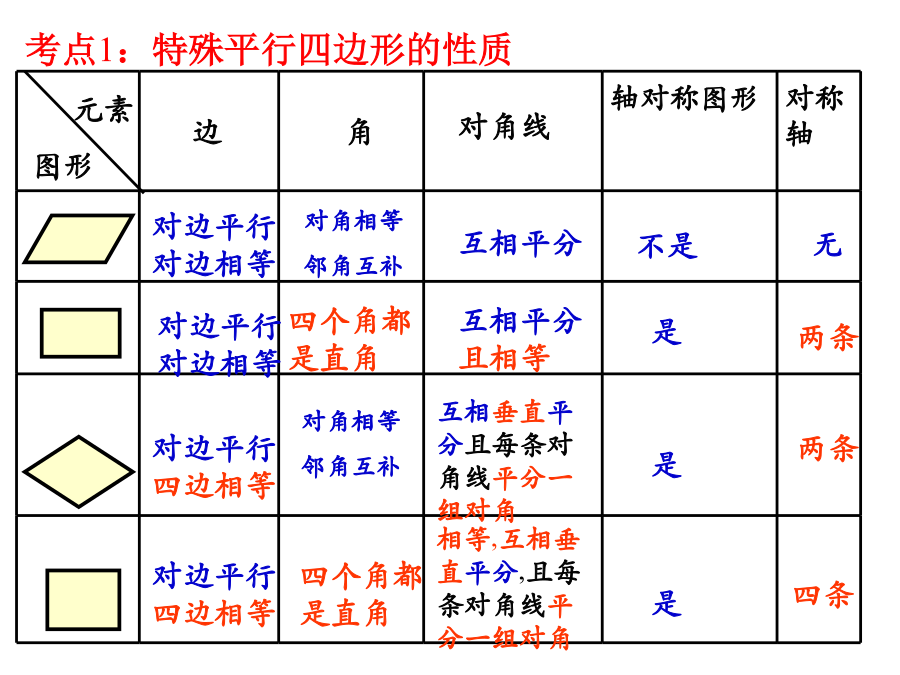
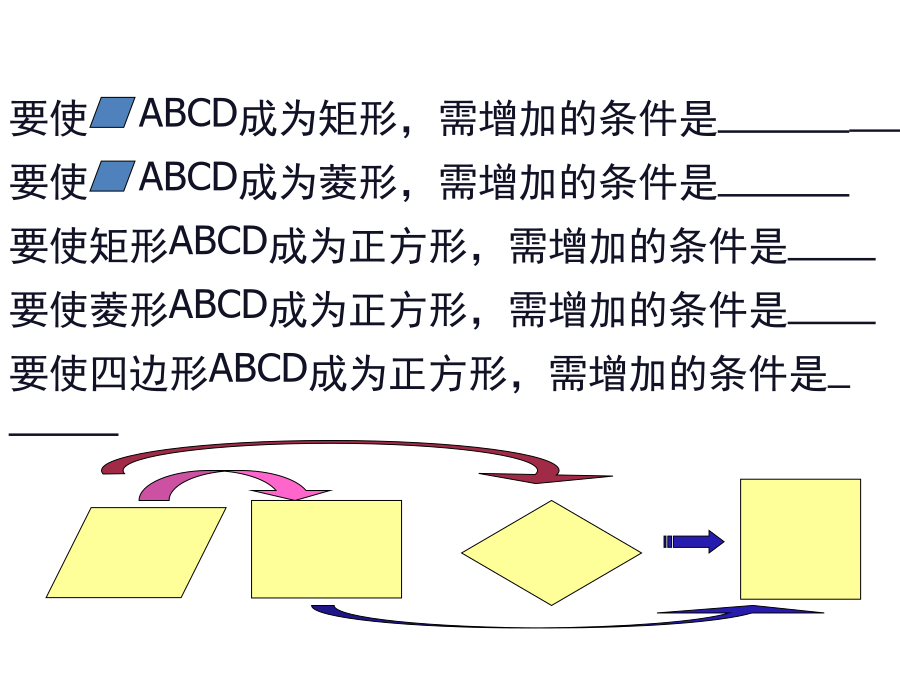
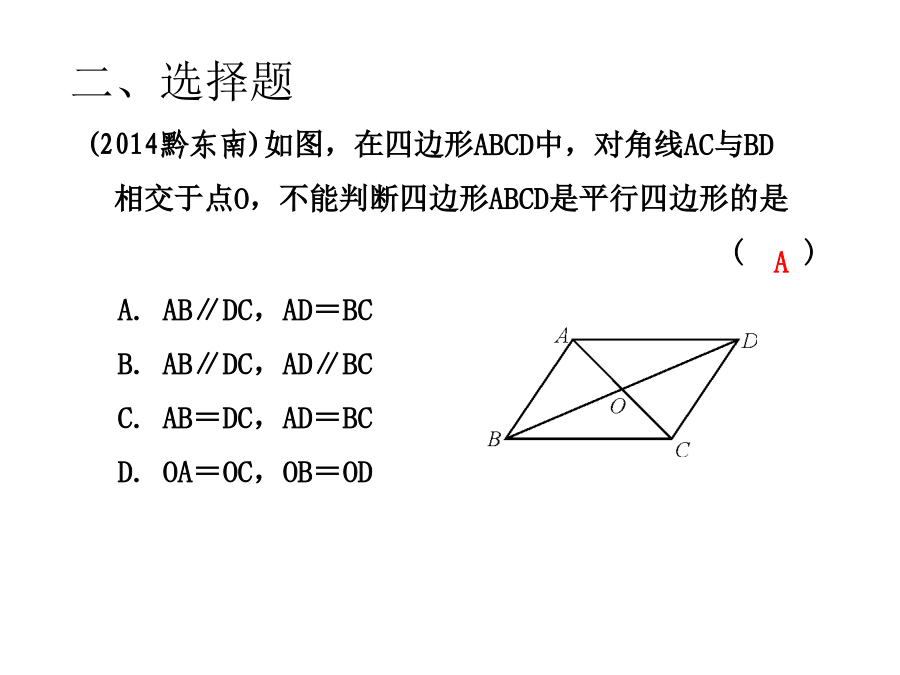
专题复习
特殊平行四边形的
性质与判定考点1：特殊平行四边形的性质考点2：特殊平行四边形的判定填空

6.两条对角线的菱形是正方形。

7.两条对角线的平行四边形是正方形。

8.两条对角线的四边形是正方形。
要使ABCD成为矩形，需增加的条件是______中考演练场一、判断题
1、对角线相等的四边形是矩形。（）
2、一组对边平行，另一组对边相等的四边形
是平行四边形。（）
3、四个角相等的四边形是正方形。（）
4、邻角相等的平行四边形是矩形。（）
5、正方形的对角线相等、垂直且平分。（）
6、对角线垂直且平分的四边形是菱形。（）
7、对角线互相垂直的矩形是正方形。（）
8、对角线相等的菱形是正方形。（）题型分类·对点训练1.如图，在ABCD中，已知点E和点F分别在AD和BC上，且AE=CF，连结CE和AF，试说明四边形AFCE是平行四边形。
3.如图，在▱ABCD中，E、F分别是边AB、CD的中点，BG∥AC交DA的延长线于点G．（1）求证：△ADF≌△CBE；（2）若四边形AGBC是矩形，判断四边形AECF是什么特殊的四边形？并证明你的结论．5.(2013•昭通)如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点（不与点A重合）,延长ME交CD的延长线于点N，连接MD，AN．（1）求证：四边形AMDN是平行四边形．（2）当AM的值为何值时，四边形AMDN是矩形？
请说明理由．（1）证明：∵四边形ABCD是菱形，∴ND∥AM，∴∠NDE=∠MAE，∠DNE=∠AME，∵点E是AD中点，∴DE=AE，在△NDE和△MAE中，
∠NDE＝∠MAE,∠DNE＝∠AME,DE＝AE，∴△NDE≌△MAE（AAS），∴ND=MA，∴四边形AMDN是平行四边形；（2）AM=1．理由如下：∵四边形ABCD是菱形，∴AD=AB=2，∵平行四边形AMDN是矩形，∴DM⊥AB，即∠DMA=90°，∵∠DAB=60°，∴∠ADM=30°，∴AM=1/2AD=1．