
二次函数的图象和性质.1.3二次函数的图象和性质 (2).doc

yy****24








在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

二次函数的图象和性质.1.3二次函数的图象和性质 (2).doc
二次函数的图象和性质及其应用教学设计一、内容和内容解析1.内容二次函数的图象和性质及其应用.2.内容解析二次函数是最基本的初等函数之一,是学习后续各类函数的基础.二次函数的核心内容是二次函数的概念、图象和性质.二次函数的图象和性质的核心,是图象“特征”、函数“特征”以及它们之间相互转化关系,这也是二次函数的本质属性所在.二次函数图象和性质,本身就是“数”与“形”的统一体.通过对图象的研究和分析,可以确定函数本身的性质,体现了数形结合的思想方法.本节课内容属于《义务教育数学课程标准(2011年版)》中的“数

二次函数y=ax2的图象和性质.1.2二次函数的图象和性质 (2).ppt
柏乡中学刘肖云1.会画二次函数y=ax2的图象2.掌握二次函数y=ax2的性质重点:二次函数y=ax2的性质难点:通过二次函数y=ax2的图象归纳其性质1.怎样画一个函数的图象?描点法:列表描点连线2.二次函数的图象是什么形状?一条抛物线二次函数的图象二次函数的图象1相同点:x函数y=-x2,y=-x2和y=-2x2的图象相同点:y=ax2当a>0时,x<0,y随着x的增大而减小。巩固提高
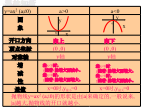
二次函数y=ax 2 k的图象与性质.1.3二次函数y=ax2 k的图象和性质.ppt
温故知新试一试:x二次函数的图像x二次函数的图象y=-x2-2函数y=ax2(a≠0)和函数y=ax2+k(a≠0)的图象形状,只是位置不同;当k>0时,函数y=ax2+k的图象可由y=ax2的图象向平移个单位得到,当k<0时,函数y=ax2+k的图象可由y=ax2的图象向平移个单位得到。(1)函数y=4x2+5的图象可由y=4x2的图象向平移个单位得到;函数y=4x2-11的图象可由y=4x2的图象向平移个单位得到.二次函数的图象课堂小结课后作业例题讲解y=ax2+ky=ax2+k课后作业

2二次函数的图象和性质.ppt
九年级上册本节课是在讨论了二次函数的图象和性质的基础上对二次函数y=ax2+bx+c的图象和性质进行研究.主要的研究方法是通过配方将y=ax2+bx+c向转化,体会知识之间内在联系.在具体探究过程中,从特殊的例子出发,分别研究a>0和a<0的情况,再从特殊到一般,得出y=ax2+bx+c的图象和性质.学习目标:1.理解二次函数y=ax2+bx+c与之间的联系,体会转化思想;2.通过图象了解二次函数y=ax2+bx+c的性质,体会数形结合的思想.学习重点:会用配方法将数字系数的二次函数的表达式化为y=的形式
二次函数图象和性质(2).ppt
二次函数的图象和性质(2)温故知新问题1分析例2解:解:解:xxxxy=-x2-2函数y=ax2(a≠0)和函数y=ax2+k(a≠0)的图象形状,只是位置不同;当k>0时,函数y=ax2+k的图象可由y=ax2的图象向平移个单位得到,当k<0时,函数y=ax2+k的图象可由y=ax2的图象向平移个单位得到。(1)函数y=4x2+5的图象可由y=4x2的图象向平移个单位得到;y=4x2-11的图象可由y=4x2的图象向平移个单位得到。当a>0时,抛物线y=ax2+k的开口,对称轴是,顶点坐标是,在对称轴的
