能带2最新固体物理学兰州大学.pptx

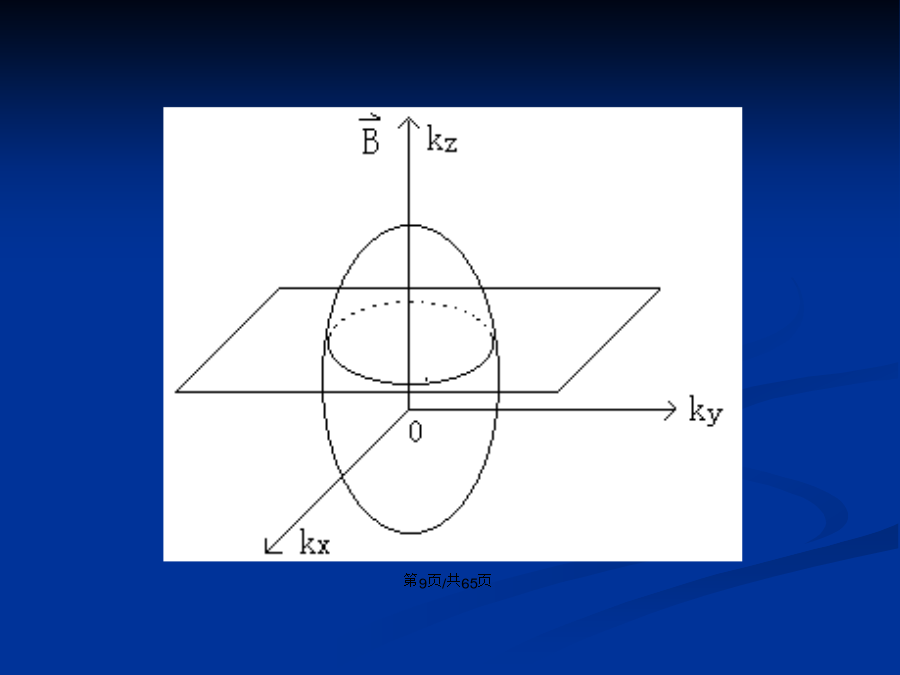
会计学2.运动方程主要考虑Bloch电子在外加电磁场下的运动规律。Bloch电子的速度是Bloch波包的群速度三维时：若外加电场为，则外场对Bloch电子要作功，在t时间内，电子的能量增加为：又∵(即电子能量的变化引起的波矢变化为k)又比较则若足够小，则有：三维时：上式表明了电子在波矢空间的运动规律。从式中可看到：电子晶体动量的变化率仅决定于外力，而与周期势场无关。（真实空间中的运动规律）（波矢空间中的运动规律）考虑Bloch电子在外加磁场下运动规律：Bloch电子的函数的形式与自由电子不同（自由电子等能面是球面）。但在能带的极值附近，可以近似展开成球面。一般说来决定于等能面的形状，而等能面的梯度决定了电子在波矢空间的速度：从上式可看出在外加磁场下，Bloch电子在波矢空间的运动规律：垂直于电子等能面的梯度。因此波矢在电子的等能面上运动。即在外加磁场下电子的能量是不变的。同时，又垂直于，说明在波矢空间的运动方向与磁场方向是垂直的。在与垂直的平面上运动。电子既要在等能面上运动，又要在垂直于的平面上运动，则只能沿这两个面的交线运动。§2.空穴电子从一个能带跃迁到上一个能带中去，在原能带中留下一个空轨道，这个空轨道称为空穴，空穴是一个几乎充满的能带中的空轨道，它是在波矢空间的能带中的概念，不是真实空间中失去电子后的空位，也不是原子离开原位置后留下的空位缺陷，在外加电磁场下，空穴的行为犹如一个带电量为+e的粒子。1.空穴的性质〈1〉空穴的波矢是失去的哪个电子波矢的负值，既一个能带若失去了一个空轨道，称为空穴，空穴的波矢空穴是描述失去了电子的能带的简捷方法，一个充满的能带失去了电子就产生了空轨道，空轨道的性质是与失去电子的能带中的集体行为联系在一起的（即拿一个电子，剩下2N-1个电子），也就是说失去了一个电子的能带既可以用2N-1个电子的集体行为来描写，也可以用一个空穴来描写，空穴的行为是与2N-1个电子的集体行为联系在一起的。空穴是假象的粒子，是准离子，主要是为了处理问题方便而引入的，空穴的性质由几乎充满的电子的集体行为所决定。〈2〉空穴的能量即空穴的能量等于失去的那个电子的能量的负值。〈3〉空穴的速度即空穴的速度与失去了的那个电子的速度相同。〈4〉空穴的有效质量即空穴的有效质量等于失去了的那个电子的有效质量的负值。电子的有效质量由电子的能带曲线的曲率来定义：有效质量是波矢k的函数，由于[空穴和电子的]能带曲线有中心反演对称性，这两条曲线的曲率是大小相等符号相反的，则可得到〈5〉在外加电磁场中空穴的运动方程如一个带电荷为+e的粒子的运动方程：2.电子和空穴在恒定电场下的半经典运动在外加恒定电场下，电子的波矢的改变满足方程式：在恒定电场中，电子的速度以均匀速度变化，若t=0时刻开始加电场，则在时刻t电子的波矢为在外加电场下t时刻电子的速度为:在BZ边界上，电子由于受Blagg反射形成驻波，驻波的速度为零，∴在BZ边界上电子的速度在一维情况下电子的速度是有界函数不象自由电子是线性函数一般情况下，对电流有贡献的不是电子的波矢变化，而是电子的速度变化，若恒定，电子的k是随时间t线性增加，而电子的速度是周期性变化的。那么在恒定电场下Bloch电子对电场响应应当是交流的，这个结果显然是错误的。这主要是我们没有考虑电子的各种散射，电子在运动过程中要与声子、晶体中的杂质等发生碰撞，这种碰撞使得把从电场中得到的定向运动的能量耗散掉使得电子在波矢空间中并不是随t的改变而线性增大。而在波矢空间中只运动一个很小的距离就停止了。也就是说电子从电场获得的能量与碰撞耗散的能量相等时就不动了。例如：则也就是说电子在外场下获得的波矢改变为，而一个BZ的尺寸，即电子的波矢改变仅为BZ尺度的。换句话说，电子只能在波矢空间在原波矢附近运动一个极小的距离。所以观察不到周而复始的变化，因而电子对外加恒定电场就不可能有周期性的响应。/在外场作用下，空穴由E到D运动到D点，D位置是空轨道，在下一时刻，电子在电场力-e（在-k方向）作用下继续向-k方向运动，空穴运动到了C点，空穴在波矢空间中与电子的运动方向是相同的，都向-k方向运动。但是空穴的波矢都沿正k方向变化（∵在波矢空间）。这个结论与空穴所满足的运动方程是一致的。半导体的价带是几乎充满的，我们用空穴来处理较方便，而导带中只有少数电子，通常直接用电子图象。半导体的总电流是指价带中的空穴电流加上导的电子电流，但这是对两个能带来讲的。§3.有效质量1.有效质量的定义一维情况下，，电子在外场作用下得到的加速度为：而由运动方程可知：或代入上式可得：或我们定义:叫作电子的有效质量,于是:具有牛顿第二定律的形式。上式说明，在外场作用下，Bloch电子要得到一个加速度，我们定义有效质量后，电子的质量不再是它的惯性质量，此时的力只包括外力而不包