
高中数学 平面向量数量积 新人教A版必修4.doc

一只****呀淑






在线预览结束,喜欢就下载吧,查找使用更方便
相关资料
高中数学 平面向量数量积 新人教A版必修4.doc
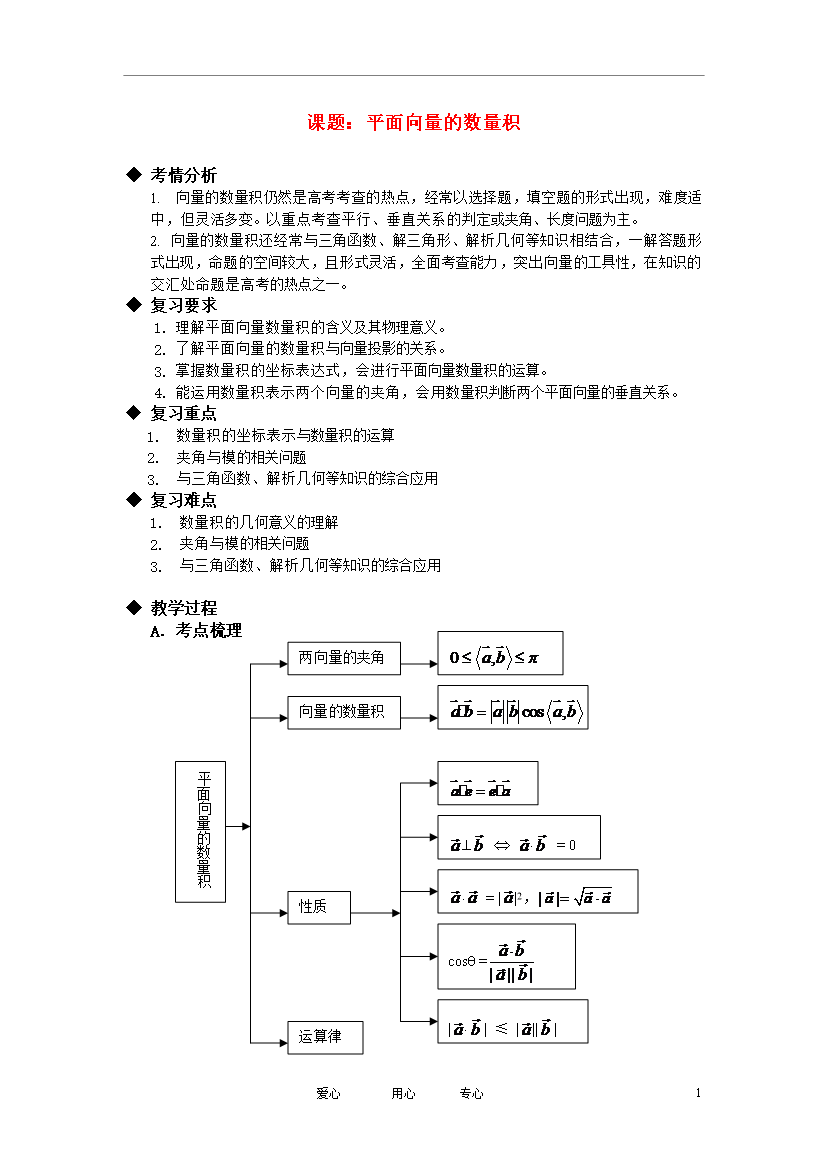
6爱心用心专心课题:平面向量的数量积考情分析向量的数量积仍然是高考考查的热点经常以选择题填空题的形式出现难度适中但灵活多变。以重点考查平行、垂直关系的判定或夹角、长度问题为主。向量的数量积还经常与三角函数、解三角形、解析几何等知识相结合一解答题形式出现命题的空间较大且形式灵活全面考查能力突出向量的工具性在知识的交汇处命题是高考的热点之一。复习要求理解平面向量数量积的含义及其物理意义。了解平面向量的数量积与向量投影的关系。掌握数量积的坐标表达式会进行平面向量数量积的运算。能运

高中数学 平面向量数量积 新人教A版必修4.doc
爱心用心专心课题:平面向量的数量积考情分析向量的数量积仍然是高考考查的热点,经常以选择题,填空题的形式出现,难度适中,但灵活多变。以重点考查平行、垂直关系的判定或夹角、长度问题为主。向量的数量积还经常与三角函数、解三角形、解析几何等知识相结合,一解答题形式出现,命题的空间较大,且形式灵活,全面考查能力,突出向量的工具性,在知识的交汇处命题是高考的热点之一。复习要求理解平面向量数量积的含义及其物理意义。了解平面向量的数量积与向量投影的关系。掌握数量积的坐标表达式,会进行平面向量数量积的运算。能运用数量积表示

高中数学_平面向量的数量积课件_新人教A版必修4.ppt
已知两个非零向量a和b,作OA=a,OB=b,则∠AOB=θ(0°≤θ≤180°)叫做向量a与b的夹角。我们学过功的概念,即一个物体在力的作用下产生位移(如图)定义注意:由向量数量积的定义,试完成下面问题:解:a·b=|a||b|cosθ=5×4×cos120°=5×4×(-1/2)=-10典型例题分析课堂练习作业:2,作业1082,1

高中数学 平面向量的数量积课件 新人教A必修4.ppt
已知两个非零向量a和b作OA=aOB=b则∠AOB=θ(0°≤θ≤180°)叫做向量a与b的夹角。我们学过功的概念即一个物体在力的作用下产生位移(如图)定注意:解:a·b=|a||b|cosθ=5×4×cos120°=5×4×(-1/2)=-10方法技巧:(1)求平面向量数量积的步骤是:①求a与b的夹角θθ∈[0°180°];②分别求|a|和|b|;③求数量积

高中数学 2.4《平面向量的数量积》教案 新人教A版必修4.doc
用心爱心专心第二章平面向量本章内容介绍向量这一概念是由物理学和工程技术抽象出来的,是近代数学中重要和基本的数学概念之一,有深刻的几何背景,是解决几何问题的有力工具.向量概念引入后,全等和平行(平移)、相似、垂直、勾股定理就可转化为向量的加(减)法、数乘向量、数量积运算,从而把图形的基本性质转化为向量的运算体系.向量是沟通代数、几何与三角函数的一种工具,有着极其丰富的实际背景.在本章中,学生将了解向量丰富的实际背景,理解平面向量及其运算的意义,学习平面向量的线性运算、平面向量的基本定理及坐标表示、平面向量的
