
第三章优化设计的某些基本概念和理论.ppt

天马****23





亲,该文档总共41页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

第三章优化设计的某些基本概念和理论.ppt
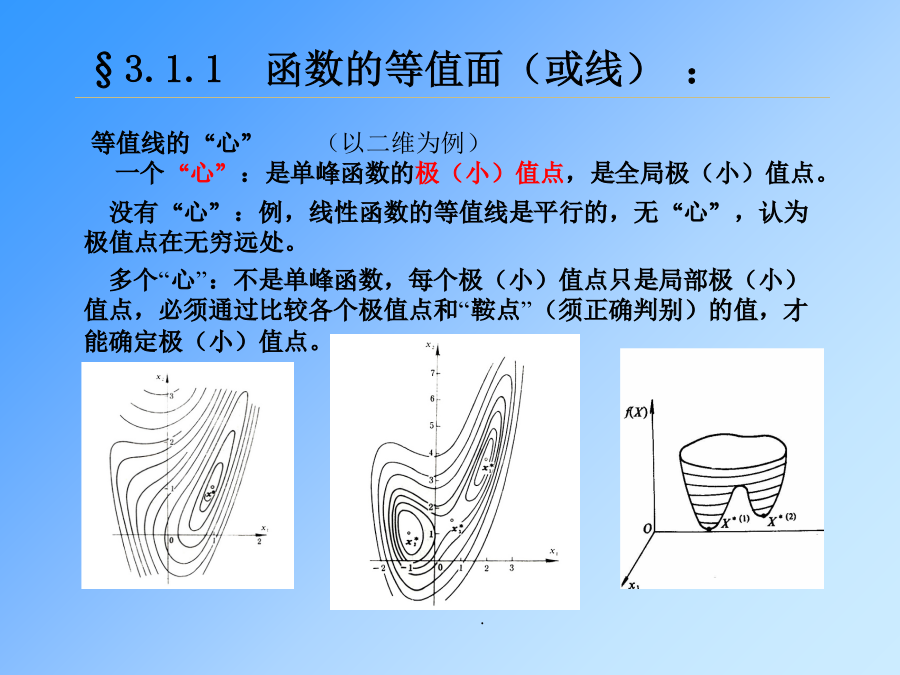
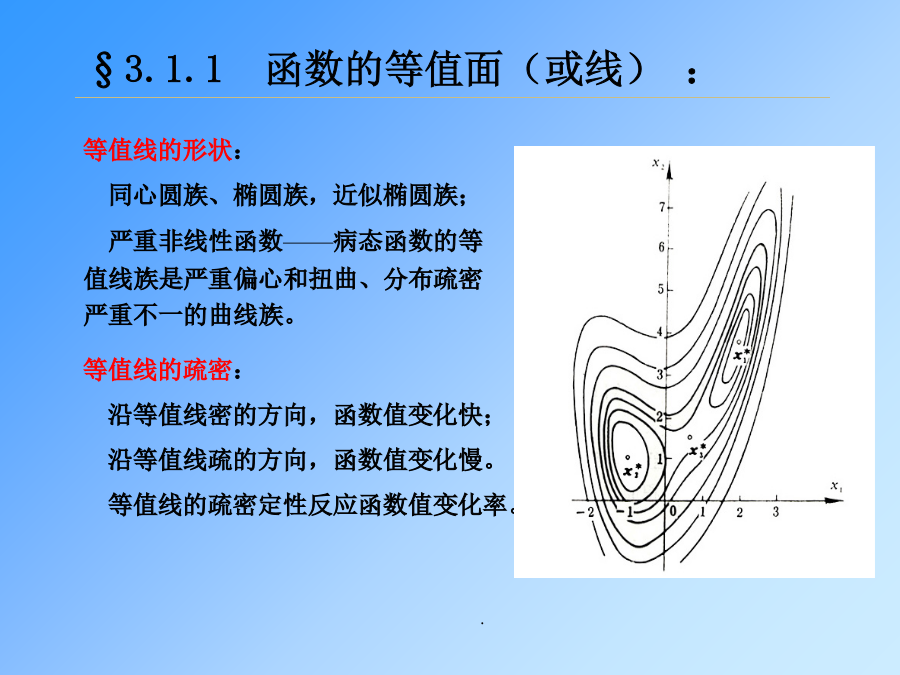
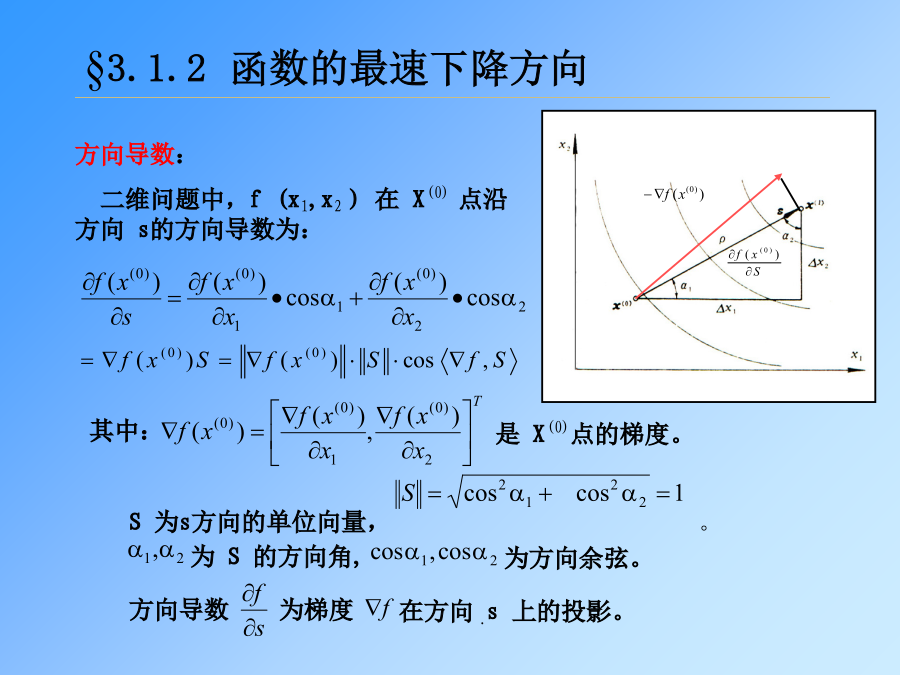
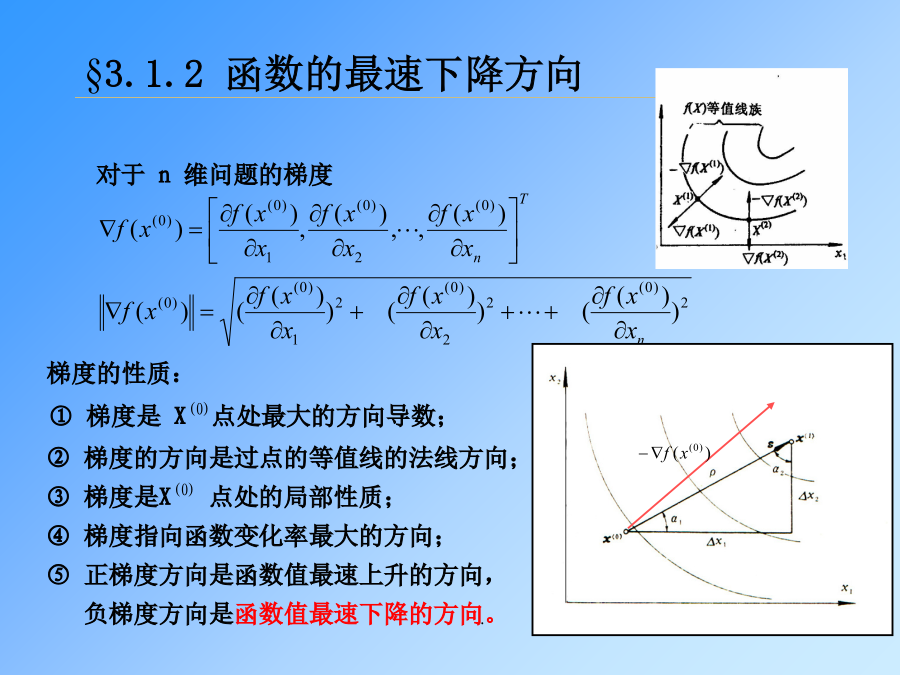
第三章优化设计的某些基本概念和处理§3.1目标函数与约束函数的某些基本性质§3.1.1函数的等值面(或线):§3.1.1函数的等值面(或线):§3.1.2函数的最速下降方向§3.1.2函数的最速下降方向§3.1.3函数局部近似的表达式和平方函数§3.1.3函数局部近似的表达式和平方函数§3.1.4函数的凸性§3.1.4函数的凸性§3.2约束函数的集合及其性质§3.2.1约束集合和可行域§3.2.1约束集合和可行域§3.2.1约束集合和可行域由此,约柬函数通过形式上的变换,结果可能丢失了函数的凸性(或者相反

第三章优化设计的某些基本概念和理论301ppt课件.ppt
第三章优化设计的某些基本概念和处理§3.1目标函数与约束函数的某些基本性质§3.1.1函数的等值面(或线):§3.1.1函数的等值面(或线):§3.1.2函数的最速下降方向§3.1.2函数的最速下降方向§3.1.3函数局部近似的表达式和平方函数§3.1.3函数局部近似的表达式和平方函数§3.1.4函数的凸性§3.1.4函数的凸性§3.2约束函数的集合及其性质§3.2.1约束集合和可行域§3.2.1约束集合和可行域§3.2.1约束集合和可行域由此,约柬函数通过形式上的变换,结果可能丢失了函数的凸性(或者相反

表面科学的某些基本概念和理论.doc
第二章表面科学的某些基本概念和理论第一节固体材料的表面一、固体材料的表面固体是一种重要的物质形态。它大致可分为晶体和非晶体两类。在固体中,原子、离子或分子之间存在一定的结合键。这种结合键与原子结构有关。固体材料的分类方法很多,例如按材料特性可分为金属材料、无机非金属材料和有机高分子材料;若按固体材料所起的作用可分为结构材料和功能材料两大类。固体表面是指固气界面或固液界面。它实际上是由凝聚态物质靠近气体或真空的一个或几个原子层(0.5-10nm)组成,是凝聚态对气体或真空的一种过渡。正是这样的原因造成了固体

优化设计的基本概念和理论.ppt
2.1机械优化设计的基本术语和数学模型例1:某公司经营两种设备。第一种设备每件售价为30元,第二种设备每件售价为450元。且知,售出第一、第二种设备分别需时为每件约0.5小时和(2+0.25x2)小时,其中x2为第二种设备售出数量。公司的总营业时间为800小时。求公司为获取最大营业额(销售额)的最优营业计划。例2:生产计划问题某工厂准备用甲、乙两台设备生产A、B两种产品。按照工艺要求,每种产品都要依次经过甲、乙设备加工。已知生产一件A产品在甲、乙两台设备上的加工时间分别为2小时和3小时,生产一件B产品在甲

优化设计的基本概念.pptx
会计学学习参考书[1]孙靖民.机械优化设计.北京:机械工业出版社,2002[2]陈立周.机械优化设计方法.北京:冶金工业出版社,1997[3]刘惟信.机械最优化设计.北京:清华大学出版社,1994第一章优化设计的基本概念优化是万物演化的自然选择和必然趋势。优化作为一种观念和意向,人类从很早开始就一直在自觉与不自觉地追求与探索。而优化作为一门学科与技术,则是一切科学与技术所追求的永恒主题,旨在从处理各种事物的一切可能的方案中,寻求最优的方案。优化的原理与方法,在科学的、工程的和社会的实际问题中的应用,便是优
