非平稳时间模型.pptx

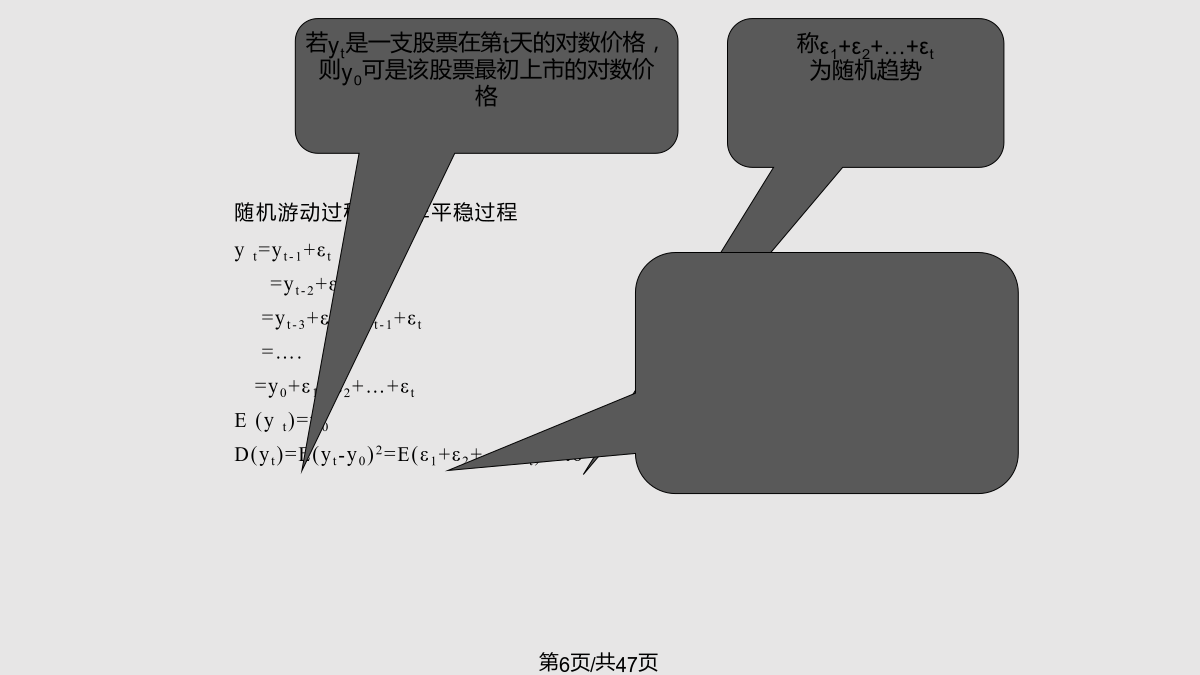
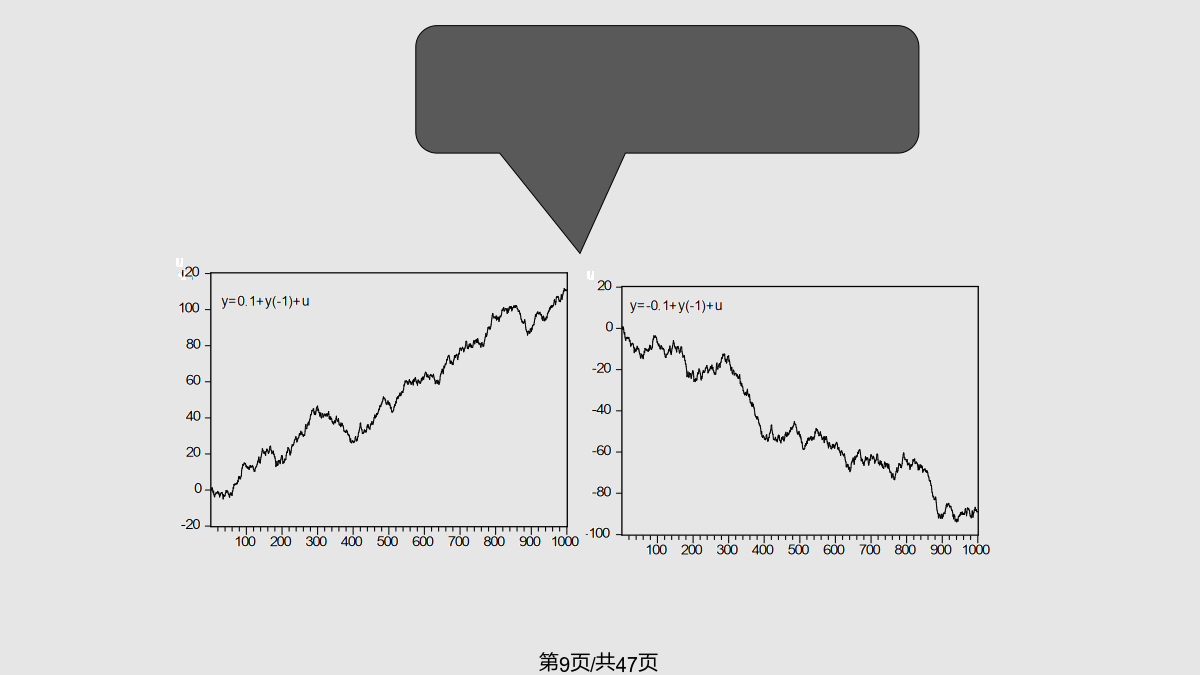
非平稳时间模型本章结构5.1、带趋势的平稳过程5.2、单位根过程随机游动过程是一非平稳过程
yt=yt-1+εt
=yt-2+εt-1+εt
=yt-3+εt-2+εt-1+εt
=….
=y0+ε1+ε2+…+εt
E(yt)=y0
D(yt)=E(yt-y0)2=E(ε1+ε2+…+εt)2=tσ2二、带常数项的随机游动过程画出xt随t变化的图像，有一个斜率为的时间趋势，且>0,xt→+∞；<0,xt→-∞
随机过程{yt,t=1,2,…},
若yt=ρyt-1+t，
其中ρ=1，
{μt}为平稳过程，E（μt）=0，
Cov（μt，μt-s）=ρs<∞,s=0,1,2,…
则称{yt}为单位根过程。yt=ρyt-1+μt，
（1-ρB）yt=μt
平稳性要求（B）=（1-ρB）=0
B=1/ρ，当ρ=1时，B=1
即有一个单位根，称为单位根过程。
当|B|>1时，|ρ|<1时，就是平稳过程。如果一个时间序列经过一次差分变成平稳的，就称原序列是一阶单整（integratedof1）序列，记为I(1)
单位根过程实际上是1阶单整过程
一般地，如果一个时间序列经过d次差分后变成平稳序列，则称原序列是d阶单整（integratedofd）序列，记为I(d)。
显然，I(0)代表一平稳时间序列。例中国支出法GDP的单整性例中国人均居民消费与人均国内生产总值的单整性yt=0.1+0.1t+yt-1+t生成的序列图考虑如下的含有一阶自回归的随机过程：
Xt=+t+Xt-1+t（*）
其中:t是一白噪声，t为一时间趋势。
1)如果=1，=0，则（*）式成为一带漂移的随机游走过程：
Xt=+Xt-1+t（**）
根据的正负，Xt表现出明显的上升或下降趋势。这种趋势为随机性趋势（stochastictrend）。
2)如果=0，0，则（*）式成为一带时间趋势的随机变化过程：
Xt=+t+t（***）
根据的正负，Xt表现出明显的上升或下降趋势。这种趋势为确定性趋势
3)如果=1，0，则Xt包含有确定性与随机性两种趋势。随机性趋势可通过差分的方法消除确定性趋势无法通过差分的方法消除，而只能通过除去趋势项消除，
如：对式
Xt=+t+t
可通过除去t变换为
Xt-t=+t
该时间序列是平稳的，因此称为趋势平稳过程
带趋势平稳过程与差分平稳过程的比较yt-t=(yt-1-(t-1))+t也就是说，对式Xt=Xt-1+t（*）做回归，如果确实发现=1，就说随机变量Xt有一个单位根。因此，可通过OLS法估计
Xt=Xt-1+t
并计算t统计量的值，与DF分布表中给定显著性水平下的临界值比较：
如果：t<临界值，则拒绝零假设H0：=0，
认为时间序列不存在单位根，是平稳的。注意：在不同的教科书上有不同的描述，但是结果是相同的。
例如：“如果计算得到的t统计量的绝对值大于临界值的绝对值，则拒绝=0”的假设，原序列不存在单位根，为平稳序列。进一步的问题：在使用上述模型
Xt=+t+Xt-1+t
对时间序列进行平稳性检验中，实际上假定了时间序列是由具有白噪声随机误差项的一阶自回归过程AR(1)生成的。
但在实际检验中，时间序列可能由更高阶的自回归过程生成的，或者随机误差项并非是白噪声，这样用OLS法进行估计均会表现出随机误差项出现自相关，导致DF检验无效。
为了保证DF检验中随机误差项的白噪声特性，Dicky和Fuller对DF检验进行了扩充，形成了ADF（AugmentDickey-Fuller）检验。ADF检验是通过下面三个模型完成的：实际检验时从模型3开始，然后模型2、模型1。同时估计出上述三个模型的适当形式，然后通过ADF临界值表检验零假设H0：=0。
1）只要其中有一个模型的检验结果拒绝了零假设，就可以认为时间序列是平稳的；
2）当三个模型的检验结果都不能拒绝零假设时，则认为时间序列是非平稳的。
这里所谓模型适当的形式就是在每个模型中选取适当的滞后差分项，以使模型的残差项是一个白噪声（主要保证不存在自相关）。例检验1978~2000年间中国支出法GDP时间序列的平稳性。从的系数看，t>临界值，不能拒绝存在单位根的零假设。
时间T的t统计量小于ADF分布表中的临界值，因此不能拒绝不存在趋势项的零假设。需进一步检验模型2。
2）经试验，模型2中滞后项取2阶：3)经试验，模型1中滞后项取2阶：例12.1.7检验关于人均居民消费与人均国内生产总值这两时间序列的平稳性。三个模型中参数的估计值的t统计量均大于各自的临界值，因此不能拒绝存在单位根的零假设。
结论：人均国内生产总值（GDPPC）是非平稳的。2）对于人均居民消费CPC时间序列来说，三个模型的适