检测技术与仪表第二章-误差分析基础ppt课件.ppt

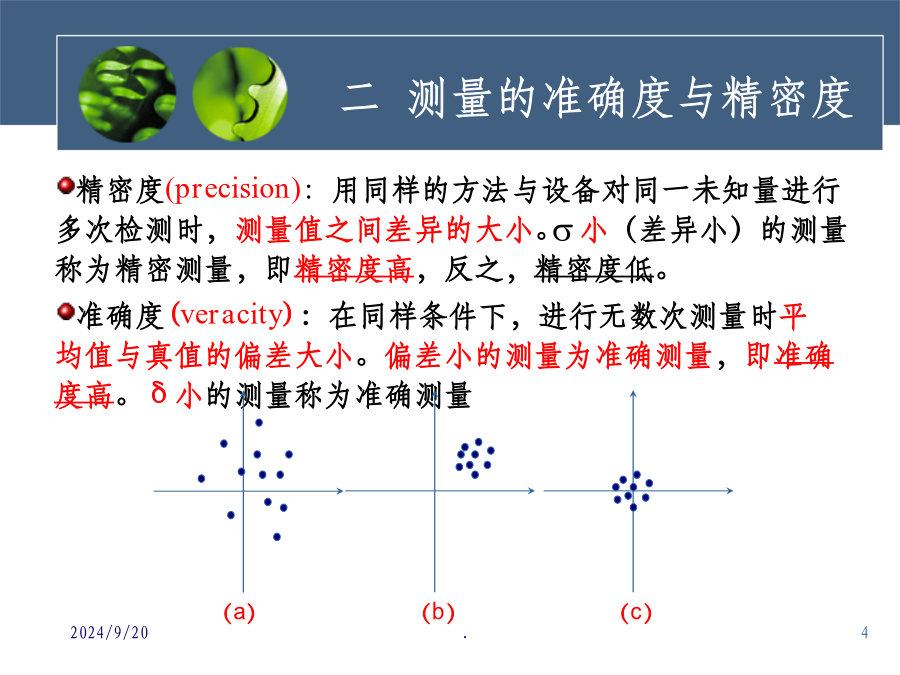
第一章误差分析基础一误差分析的基本概念2几种误差的定义二测量的准确度与精密度例：两组测量数据：
第一组：1.23,1.32,1.08,1.26.1.14
第二组：1.23,1.22,1.23,1.22,1.22
δ1=0.006如图，曲线1和2是两条测量数据分布曲线。A为被测量的真值，Aa为一种测量方法测得的平均值，Ab为另一种测量方法测得的平均值，分析得知：
曲线1表示准确却不精密（误差小，标准误差大）；
曲线2表示精密却不准确（误差大，标准误差小）。
只有准确度和精密度都高，才能称为精确的测量。三误差原因分析四误差的分类随机误差(randomerror)
1.定义：相同条件下多次重复测量同一量时，误差的大小和符号是无规律变化的误差。
2.产生的原因：是由测量过程中互相独立的、微小的偶然因素引起的。
3.消除：不能消除，也不能修正，值是随机的。
4.特点：多次重复测量时，总体服从统计规律，故可以了解它的分布特性，并能对其大小和测量结果的可靠性作出估计，是误差理论的依据。粗大误差(crassierror)
1.定义：相同条件下多次重复测量同一量时，明显偏离了结果的误差。
2.产生的原因：疏忽大意或不正确的观测、测量条件的突然变化、仪器故障等。
3.消除：遵循一定的规则。
4.特点：通常数值比较大。测量中应避免这类误差的出现。粗大误差也称为坏值，应该剔除。判断某一测量值是否为坏值，可用统计方法或遵循一些准则。检验坏值的方法：{五随机误差的统计特性2.随机误差的统计性质
对称性：绝对值相等的正误差和负误差出现的次数相等。故f(x)为偶函数，其分布曲线对称纵轴。
单峰性：绝对值小的误差比绝对值大的误差出现次数多绝对值小的误差概率密度大;
抵偿性：随测量次数增加，随机误差的代数和为零，即正负误差相互抵消。
有界性:在一定的测量条件下，随机误差的绝对值不会超过一定界限，即绝对值很大的误差基本不发生。随机误差的概率密度分布曲线f(x)满足：作业