离散变量优化问题.pptx

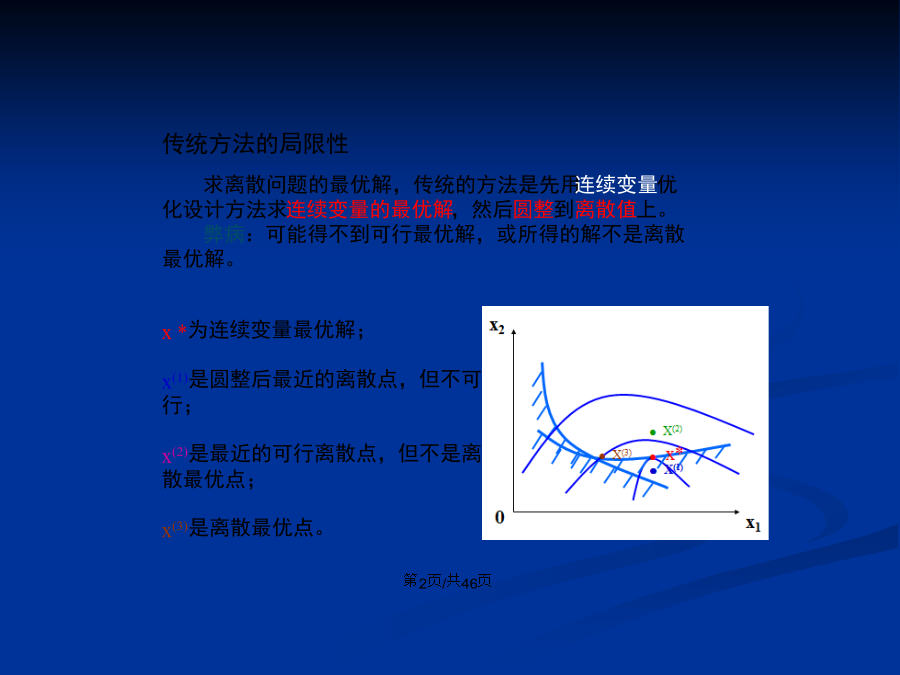
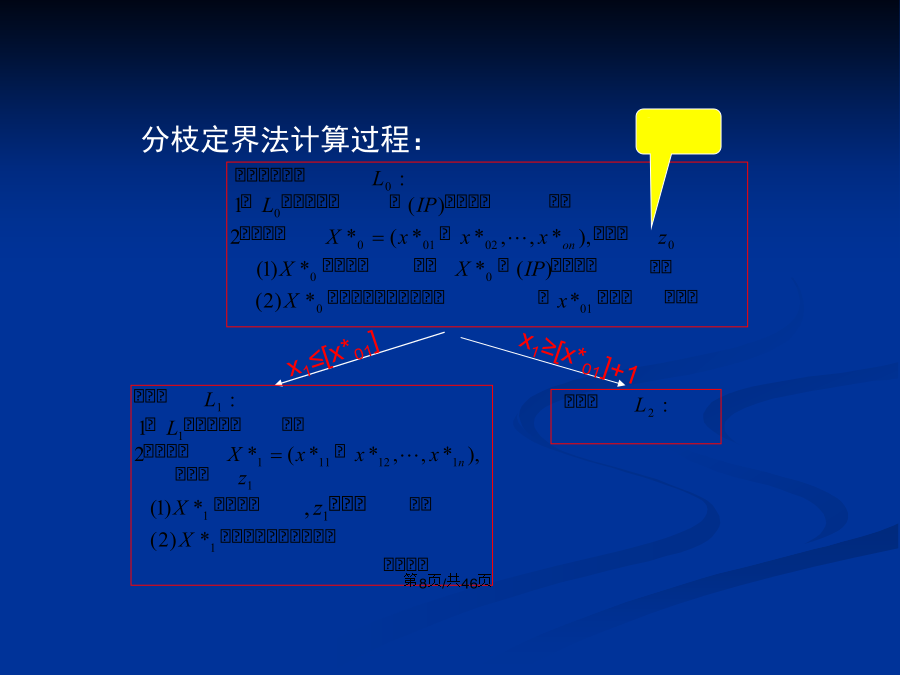
会计学一般的优化方法只能求得连续变量的最优解。
工程实际中存在大量混合设计变量问题。
混合设计变量包含：连续设计变量、整型设计变量和离散设计变量。求离散问题的最优解，传统的方法是先用连续变量优化设计方法求连续变量的最优解，然后圆整到离散值上。
弊病：可能得不到可行最优解，或所得的解不是离散最优解。离散变量优化难点：不存在指导搜索过程的最优性条件。

直接方法：枚举法（enumeration）。可行点过多时，计算量大。

减少计算量：随机思想（stochasticideas）、启发式原则（heuristicrules）。

两种基本方法：
（隐式）枚举法：如，分枝定界法（thebranchandboundalgorithm）；
随机或进化方法：如，模拟退火算法、遗传算法等。§9.3分枝定界法（thebranchandboundalgorithm）分枝定界法基本思想：
设有最大化的整型优化问题A，相应有松弛问题B，从解松弛问题B开始，若其最优解不符合A的整数条件，那么B的最优目标函数必是A的最优目标函数的上界，记作；而A的任意可行解的目标函数值将是的一个下界，记作。
分枝定界法就是将B的可行域分成子区域(称为分枝)的方法，逐步减小，增大，最终求到。（1）分枝
在松弛问题B的最优解中任选一个不符合整数条件的变量,其值为,以表示小于的最大整数。构造两个约束条件
（2）定界
以每个后继问题为一分枝标明求解结果,在解的结果中,找出最优目标函数值最大者作为新的上界.从已符合整数条件的各分支中,找出目标函数值为最大者作为新的下界,若无,则下界为0.

（3）比较与剪枝
各分支的最优目标函数中若有小于，则剪掉这枝；若大于且不符合整数条件，则重复前两步，直到找到最优解。分枝定界法计算过程：例：用分枝定界法求解整型优化问题（用图解法计算）：求出松弛问题最优解：/先将（LP）划分为（LP1）和（LP2）,取。现在只要求出（LP1）和（LP2）的最优解即可。/先求（LP1）,如图所示。先求（LP1）,如图所示。/求（LP2）,如图所示。∵Z(2)>Z(1)=16，
∴原问题可能有比（16）更大的最优解；
但x2不是整数，故利用x2≤3，x2≥4加入条件。现在只要求出（LP21）和（LP22）的最优解即可。/先求（LP21）,如图所示。求（LP22），如图所示。
无可行解，不再分枝。LP21取得最优解：

且有
x1＝2.4不是整数，可继续分枝，令x1≤2，x1≥3。现在只要求出（LP211）和（LP222）的最优解即可。先求（LP211）先求（LP211）求（LP212）/找到最优解（1）若分枝后得到整数解，则这枝不必再分枝；
（2）若分枝后得到非整数解,如果比整数解更好，则这枝继续分枝；
（3）若分枝后得到非整数解,如果比整数解更差，则这枝不必再分枝。§9.3离散变量优化——组合形法以复合形法为基础发展而来，使之能在离散空间中直接搜索离散点，从而满足求解离散变量优化问题的需要。

基本思想：通过对初始复合形调优迭代．使新的组合形不断向最优点移动和收缩，直至满足一定的终止条件为止。

下面分五个部分介绍离散变量组合形法：
（1）初始离散组合形的产生
（2）离散一维搜索
（3）约束条件处理
（4）组合形的调整
（5）收敛准则§9.3.1初始离散组合形的产生§9.3.2离散一维搜索§9.3.2离散一维搜索（续）§9.3.3约束条件的处理§9.3.4辅助功能和终止准则§9.3.4辅助功能和终止准则（续）§9.3.5离散变量组合形算法基本步骤///THEEND