多目标及离散变量优化方法.ppt

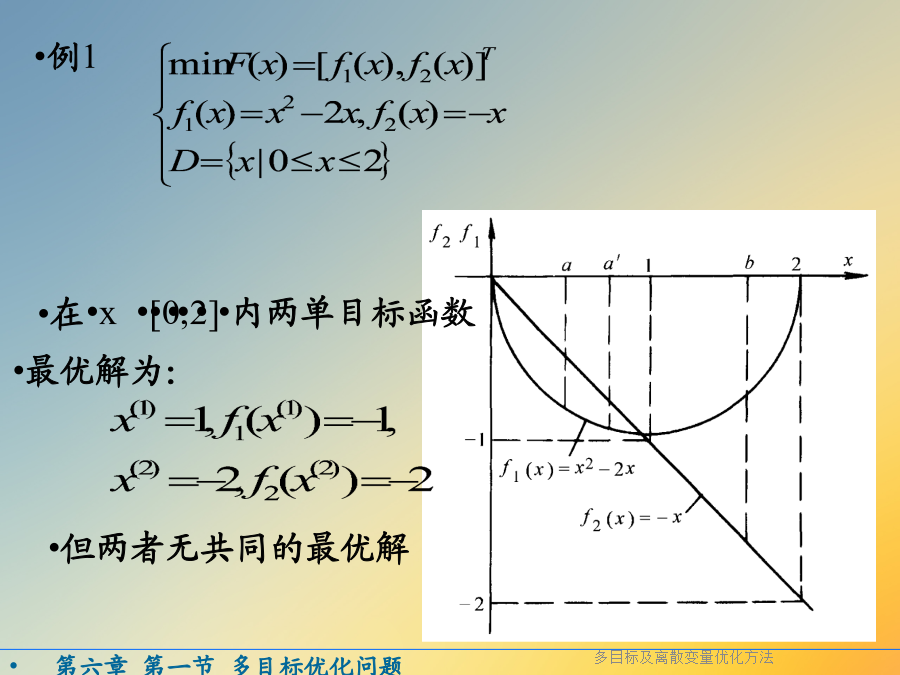
多目标及离散变量优化方法第六章多目标优化方法和离散变量优化方法简介第六章重点内容第六章机械设计中，同时要求几项设计指标达到最优的问题
——多目标优化设计问题判别方案的优劣：
单目标：只要用f(x)去比较即可例1①一、主要目标法
基本思想：多个目标中选择一个目标作为主要目标，而其它目标则只需满足一定的要求即可，即将目标转化为约束条件
目标函数转化为：1．线性加权法
基本思想：将各个分目标函数为消除各分目标在量级上的差别，先将分目标函数fi(x)转化为无量纲等量级目标函数设各分目标函数值的变动范围为：其中，
w1i——本征权因子，反映各分目标的重要程度
w2i——校正权因子，调整各分目标间量级差别的影响基本思想：先定出各分目标函数的最优值，根据多目标优化设计的总体要求对这些最优值进行调整，定出各分目标的最合理值V——基本思想：对应每一目标函数都用功效系数功效系数的确定方法：③指数法基本思想：多目标优化问题中，存在目标函数间相互矛盾的情况，一个（些）目标函数值的减小，将导致另一个（些）目标函数值的增大。因此，各分目标函数值之间需要进行协调，以便取得合理的方案。
如图所示，两维双目标函数f1(x)、f2(x)的等值线和两个不等式约束曲面.f1(x)最优点T点，f2(x)最优点P点
可行域中任意一点R.
从R点起沿f1(x)=5等值线，向约束面移动f2(x)不断改善，
直至边界上S点。
从R点起沿f2(x)=8等值线，向约束面f1(x)移动不断改善，
直至边界上Q点。该曲线反映了两个设计目标全部最佳方案的调整范围,再建立一个衡量设计方案满意程度的准则，建立一组反映不同满意程度的曲线u(f1,f2)，使随着满意度增加，同时使目标函数f1(x)和f2(x)都有所下降。
满意度曲线与协调曲线的切点，即为最优设计方案。如图所示O点
满意度曲线不同，则最优设计方案也不同。基本思想：将多目标优化问题的各目标函数按重要程度排列，然后，依次对各个目标函数求最优解，而后一目标函数应在其前面目标函数最优解的集合域内寻优。
1、分层序列法
设分目标函数重要程度次序为：f1(x)、f2(x)，…
则首先对f1(x)寻优：2、宽容分层序列法
基本思想：即先对各目标函数的最优值取一定的宽容量ε1，ε2，…，εl(>0)，使求后一个目标函数最优值时，对前一些目标函数的约束扩大为在其最优值附近的某一范围内。例1用宽容分层序列法求解等间隔的离散变量
非均匀间隔离散变量
→特例：整数变量—整数规划问题

最简单处理办法：按连续变量处理，得最优解后，再圆整为最近的离散值

问题：①圆整后的点在非可行域;
②圆整为哪一个附近的离散值难于确定;
③有些情况下设计变量不允许最后取整。式中二、约束非线性离散变量的优化方法
常用方法：
1)以连续变量优化为基础的方法：
圆整法、拟离散法、离散型罚函数法
2)离散变量随机优化方法：
随机试验法，随机离散搜索法
3)离散变量搜索优化方法：
组合优化法，整数梯度法
4)其它离散变量优化方法：
非线性隐枚举法，分支定界法

(一)以连续变量优化为基础的方法
1、整型化、离散化法
基本思想：先按连续变量方法求得最优解x*，再进一
步寻找整型量或离散量优化解。设最优点2．拟离散法
基本思想：在求得连续变量最优解x*后，在x*点附近按一定方法进行搜索来求得优化离散解。
(1)交替查找法：适于全整数变量优化问题（略）
(2)离散分量取整，连续分量优化法：
适用于混合离散变量优化问题（略）离散惩罚函数定义方法:2）将离散惩罚函数项Qk(xD)加到内点法SUMT的惩罚项中，得离散惩罚函数为：例1求f(x)=x/2的最小整数优化解，约束函数
g1(x)=1.3-x≤0
如图所示，分别表示k不同时，方法缺点：离散惩罚函数易出现病态，使优化搜索带
来困难。
(二)离散变量搜索型方法——离散复合形法
特点：在离散空间直接搜索，每次得到的复合形顶点都是离散点，通过不同的搜索方法来改变其形状，使复合形逐步向离散最优点趋近。
算法步骤：
1)在n维空间产生由2n+1个顶点构成的初始复合形，并将各顶点移到各自附近的离散点上。
2)将各项点按目标函数值由大到小排列，找出最坏点AH
3)找出除最坏点外复合形的几何中心，并求出最坏点AH相对于中心点的反射点Ap并移到附近离散点上。
4)如Ap点可行，且目标函数值比AH点好，则用Ap替代AH点，组成新复合形→转步骤2否则，沿反射的反方向搜索定新点。
5)如用上述方法失败，则依次用次坏点…代替最坏点
作为映射点，转步骤3）
6)如用最好点代替AH作为映射点，仍找不到好点，或
复合形退化到n-1维空间时，表示算法收敛。此时，
取复合形顶点中最好的点作为离散优化解。
(三)离散变量型网格法
1.离散变量型普通网格法
基本思想：以一定的