内容提供者
矩阵特征值分解与奇异值分解.ppt
2024-09-16
10金币
283KB
15页
天马****23
实名认证
内容提供者
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
亲，该文档总共15页，到这已经超出免费预览范围，如果喜欢就直接下载吧～
相关资料
矩阵特征值分解与奇异值分解.ppt
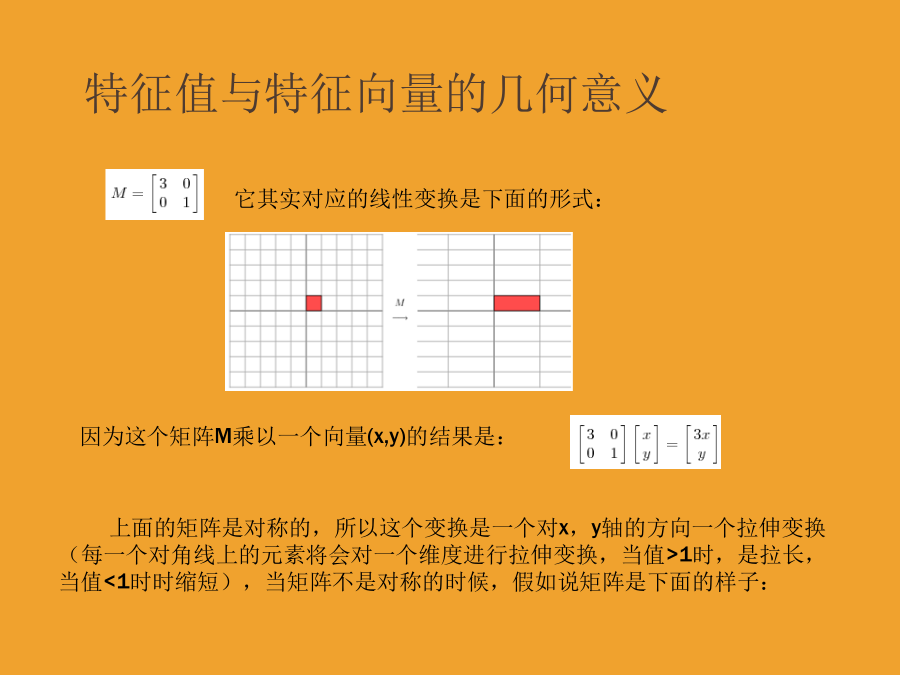
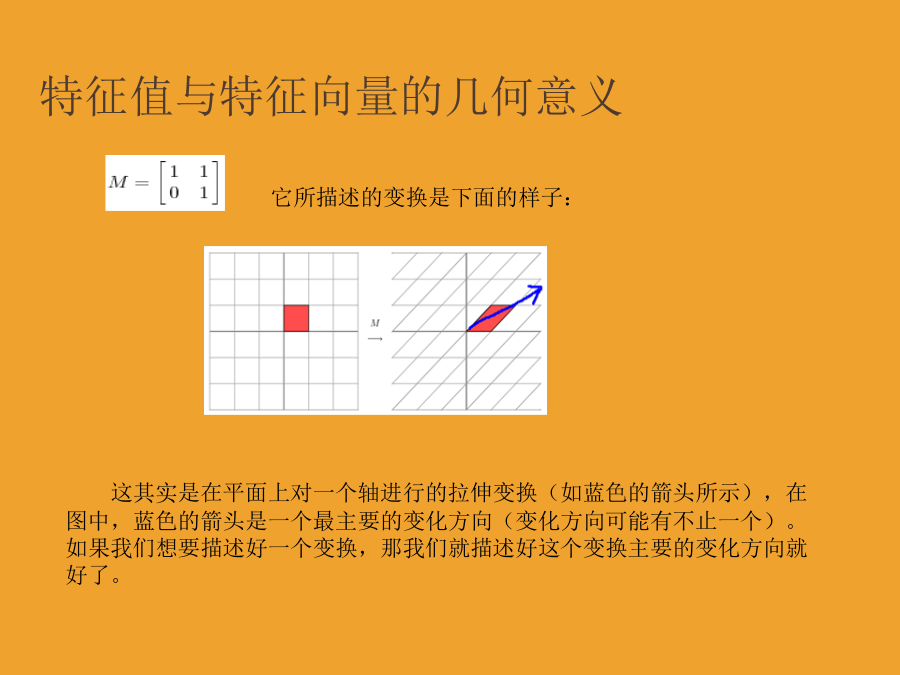
矩阵特征值分解与奇异值分解特征值与特征向量的几何意义特征值与特征向量的几何意义特征值与特征向量的几何意义特征值分解特征值分解奇异值分解奇异值分解奇异值分解奇异值分解奇异值分解奇异值与主成分分析（PCA）：奇异值与主成分分析（PCA）：奇异值与主成分分析（PCA）：更多内容请参考：http://220.169.242.165:8080/TEST8/VIP/h_goto.php?u=wudi123124
2024-09-16
10
283KB
矩阵分解矩阵的奇异值分解课件学习.pptx
会计学定义2.19设,若,则称A为酉矩阵.定义2.20设,若存在酉矩阵P,使得,则A称酉相似于B.性质1若A是n阶实对称矩阵，是的特征值，则恒存在正交阵Q，使得而且Q的n个列向量是的一个完备的标准正交特征向量系。性质2若，是非奇异矩阵，则存在正交阵P和Q，使得其中.性质3(1)设,则是Hermit矩阵,且其特征值均是非负实数;(2);(3)设,则的充要条件为.把性质2中的等式改写为称上式是A的正交对角分解.性质4(1)设,则A酉相似于对角阵的充分必要条件是A为正规矩阵;(2)设,且A的特征值都是实数,则正
2024-10-10
20
273KB
矩阵的奇异值分解.docx
§2矩阵的奇异值分解定义设是秩为的复矩阵，的特征值为.则称为A的奇异值.易见，零矩阵的奇异值都是零，矩阵的奇异值的个数等于的列数，的非零奇异值的个数等于其秩.矩阵的奇异值具有如下性质：（1）为正规矩阵时，的奇异值是的特征值的模；（2）为半正定的Hermite矩阵时，的奇异值是的特征值；（3）若存在酉矩阵，矩阵，使，则称A和B酉等价.酉等价的矩阵A和B有相同的奇异值.奇异值分解定理设是秩为的复矩阵，则存在m阶酉矩阵与n阶酉矩阵，使得.①其中，为矩阵的全部非零奇异值.证明设Hermite矩阵的n个特征值按大小
2024-11-08
20
270KB
矩阵的奇异值分解.pdf
§2矩阵的奇异值分解T定义设A是秩为r的mn复矩阵，AA的特征值为12rr1n0.则称ii(i1,2,,n)为A的奇异值.易见，零矩阵的奇异值都是零，矩阵A的奇异值的个数等于A的列数，A的非零奇异值的个数等于其秩.矩阵的奇异值具有如下性质：（1）A为正规矩阵时，A的奇异值是A的特征值的模；（2）A为半正定的Hermite矩阵时，A的奇异值是A的特征值；mmnnmn（3）若存在酉矩阵UC,VC，矩阵BC，使UAVB，则称A和B酉等价.酉等价的矩阵A和B有相同的奇异值.奇异值分解定理设A是秩为r(r0)的mn
2024-08-16
8
109KB
矩阵奇异值分解.ppt
第三节奇异值分解矩阵的等价标准型引理1证明设x是方程组AHAx=0的非0解，对于Hermite矩阵AHA，AAH，设AHA，AAH有r个非0特征值，分别记为奇异值的定义定理酉等价的矩阵有相同的奇异值称为矩阵A的酉等价标准形.证明比较等式两端得：即U1的r个列是两两正交的单位向量，则于是推论在矩阵A的奇异值分解A=UDVH中，U的列向量为AAH的特征向量，V的列向量为AHA的特征向量.1]求矩阵AHA的酉相似对角矩阵及酉相似矩阵V;例1、求矩阵构造：奇异值分解方法2--利用矩阵AAH求解例求矩阵A的奇异值分
2024-08-17
10
384KB