用灰色模型进行数学建模.ppt

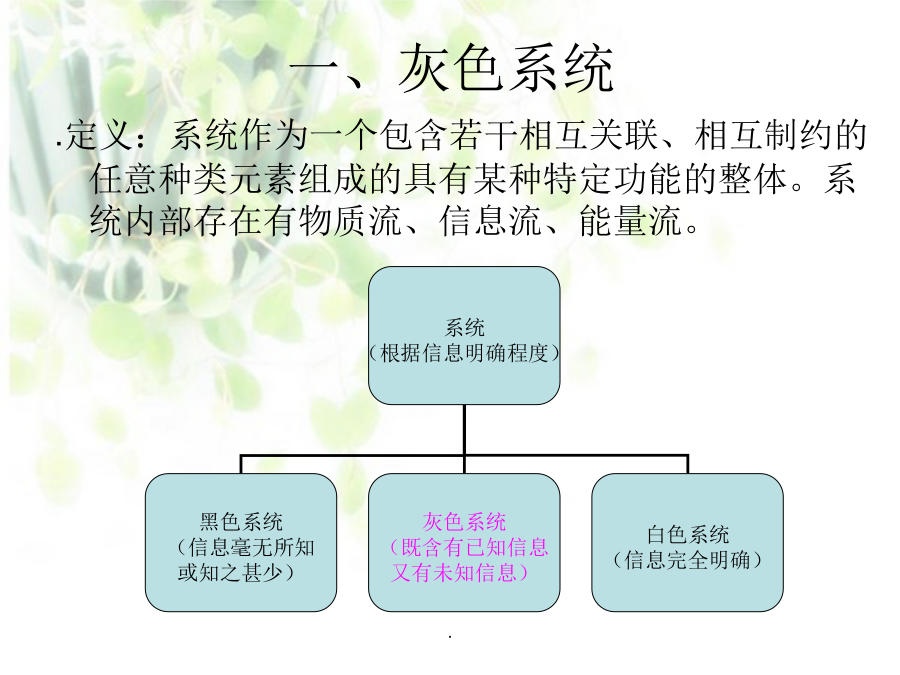
数学建模中的灰色方法在数学建模的过程中，常常遇到一些诸如：人口模型、全国的物资调运、运输、生产销售等问题，其中有许多信息都无法确定，要建立这样的模型很困难。
现有的系统分析方法—量化分析方法，大都是数理统计方法但这种方法多用于少因素的、线性的情形。对于多因素的、非线性的则难以处理。
针对这些不足，邓聚龙教授创立了一种就数找数的方法，即灰色系统生成法。创立灰色系统的学科体系和灰色系统“概念与公理体系”，提出灰生成空间、灰关联空间理论、灰建模理论并创立灰预测理论及方法体系。一、灰色系统（一）灰色系统公理：
1.信息不完全、不确定的解是非唯一的；（解的非唯一性原理）
2.信息是认识的根据；（认识根据原理）
3.灰色系统理论的特点是充分开发利用已占有的“最小信息”；（最小信息原理）
4.新信息对认识的作用大于老信息；（新信息优先原理）

（二）灰色系统的描述：
灰色系统用灰色参数、灰色方程、灰色矩阵、灰色度等综合描述，其中灰数是灰色系统的基本单元。1.灰色参数（灰数）
灰数是那些只知道大概范围而不知其确切值的数（只知道部分数学特征，而不知道具体数值的参数）。例如：“某人的身高约为170cm、体重大致为60kg”，这里的“（约为）170（cm）”、“60”都是灰数，分别记为、。又如，“那女孩身高在157－160cm之间”，则关于身高的灰数。
记为灰数的白化默认数，简称白化数。在灰色系统理论中，把随机变量看成灰数，即是在指定范围内变化的所有白色数的全体。如代购一件价格为100元左右的衣服，100可作为预购衣服价格的白化值。
灰数有离散灰数（属于离散集）和连续灰数（属于某一区间）。
2.灰色代数方程—含有灰色系数的代数方程
如：

灰色微分方程为含有灰色导数或灰色微分的方程，如

3.灰色矩阵—行列数确知而含有灰元的矩阵
若在A的m*n个元素中，有N个灰色元素，则可以用d表示这一矩阵的灰色度
二、灰色生成数列（1）累加生成
把数列各项（时刻）数据依次累加的过程称为累加生成过程（AGO）。由累加生成过程所得的数列称为累加生成数列。
设原始数列为，令

称所得到的新数列
为数列的1次累加生成数列。类似地有

称为的r次累加生成数列。（2）累减生成
对于原始数据列依次做前后相邻的两个数据相减的运算过程称为累减生成过程IAGO。如果原始数据列为

令
称所得到的数列为的1次累减生成数列。

注：从这里的记号也可以看到，从原始数列，得到新数列，再通过累减生成可以还原出原始数列。实际运用中在数列的基础上预测出，通过累减生成得到预测数列。（3）加权邻值生成
设原始数列为
称为数列的邻值。
为后邻值，为前邻值，对于常
数，令

由此得到的数列称为数列在权下的邻值生
成数，权也称为生成系数。
特别地，当生成系数时，则称

为均值生成数，也称等权邻值生成数。灰色系统理论的主要方法三、灰色预测模型GM(m,n)(一)GM（1，1）模型即或（1）

在式（1）中，称为灰导数，a称为发展系数，称为白化背景值，b称为灰作用量。
将时刻表代入（1）式有

引入矩阵向量记号：

数据向量参数向量数据矩阵于是GM（1，1）模型可表示为
现在问题归结为求a,b在值。用一元线性回归，即最小二乘法求它们的估计值为

注：实际上回归分析中求估计值是用软件计算的，有标准程序求解，如matlab等。
GM（1，1）的白化型
对于GM（1，1）的灰微分方程（1），如果将灰导数的时
刻视为连续变量t，则视为时间t函数，于是对应于导数量级，白化背景值

对应于导数。于是GM（1，1）的灰微分方程对应于的白微分方程为
（2）
（二）GM（1，1）灰色预测的步骤2.建立GM（1，1）模型
不妨设满足上面的要
求，以它为数据列建立GM（1，1）模型

用回归分析求得a,b的估计值，于是相应的白化模型为

解为（4）

于是得到预测值

从而相应地得到预测值：3.检验预测值
（1）残差检验：计算相对残差

如果对所有的，则认为达到较高的要求：否则，若
对所有的，则认为达到一般要求。
（2）级比偏差值检验：计算

如果对所有的，则认为达到较高的要求；否则
若对所有的，则认为达到一般要求。四、应用举例究竟SARS疫情对
商品零售业、旅游业、
综合服务业的影响有
多大,已知某市从1997
年1月到2003年12月
的商品零售额、接待
旅游人数、综合服务
收入的统计数据如图:2.模型分析
根据所掌握的历史统计数据可以看出，在正常情况下，全年的总和（或平均值）较好地反映了相关指标的变化规律。从而我们把预测分成两部分：利用灰色理论建立GM(1,1)模型，由1997－2002年的各年度总和值预测2003年的年度总和值；再通过历史数据计算每个月的指标值与全年总和的关系，就可以预测出200