
一种嵌入式裁床控制器的实时轮廓误差补偿方法.pdf

猫巷****雪凝






在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

一种嵌入式裁床控制器的实时轮廓误差补偿方法.pdf
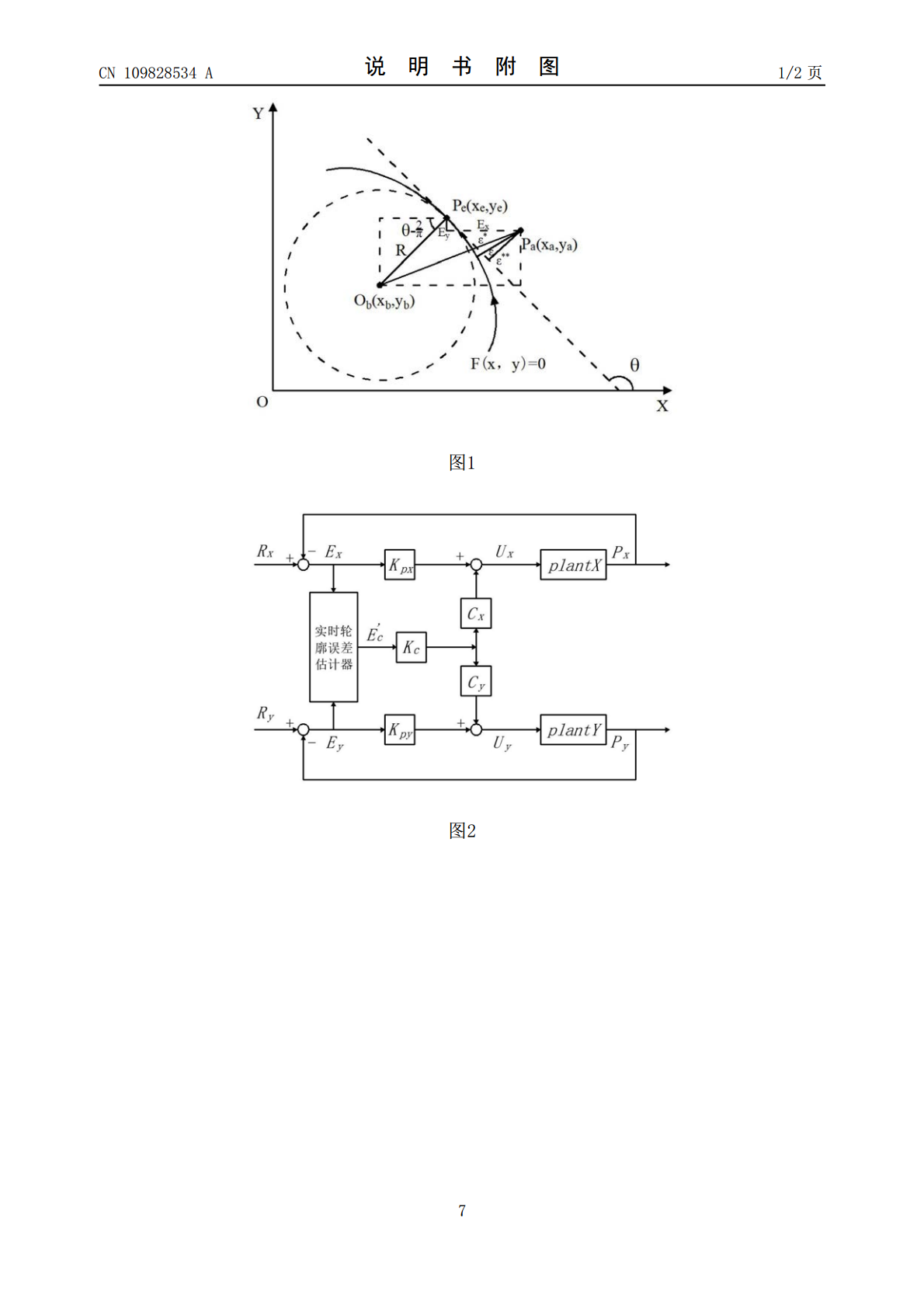
一种嵌入式裁床控制器的实时轮廓误差补偿方法,包括如下步骤:通过编码器反馈的当前位置和期望位置之间的偏差,得到X轴和Y轴的直接位置误差E

一种实时轮廓误差估算方法及其预补偿仿真.docx
一种实时轮廓误差估算方法及其预补偿仿真Title:AReal-timeContourErrorEstimationMethodanditsPre-compensationSimulationAbstract:Theaccurateestimationofcontourerrorsiscrucialinvariousfieldssuchascomputervision,robotics,andmanufacturing.Thispaperproposesareal-timecontourerrorestim

一种随动与轮廓误差自适应实时补偿方法.pdf
一种随动与轮廓误差自适应实时补偿方法,属于精密高效智能化数控加工技术领域,涉及数控参数曲线插补加工过程中一种基于进给系统在线辨识的随动误差自适应补偿方法及一种基于高精度轮廓误差实时估计的轮廓误差补偿方法。该方法采用最小二乘法对数控进给系统进行在线辨识,根据辨识结果自适应补偿随动误差,再根据实际刀位点计算轮廓误差估计值,并对轮廓误差进行进一步直接补偿,实现随动与轮廓精度的同步提高。该补偿方法可提高数控机床单轴跟踪精度及多轴联动加工轮廓精度,误差抑制效果好,适应性强,对提高数控机床加工精度、实现复杂曲面类零件

空间曲线轮廓误差实时估算与补偿方法研究.docx
空间曲线轮廓误差实时估算与补偿方法研究空间曲线轮廓误差实时估算与补偿方法研究摘要:随着制造技术的发展,越来越多的零件已经脱离了二维制造时代,进入了三维制造时代。但是相比于二维制造,三维制造所需的精度更高、复杂度更大,对加工设备和工具的稳定性和精度要求更高。本文提出了一种新的空间曲线轮廓误差实时估算与补偿方法,可以在保证工件精度和质量的同时,提高零部件的加工效率与精度。关键词:空间曲线、轮廓误差、实时估算、补偿方法一、研究背景随着制造技术的日新月异,越来越多的产品已经脱离了二维制造时代,进入了三维制造时代。

一种裁床的位图轮廓坐标提取方法.pdf
一种裁床的位图轮廓坐标提取方法,包括如下步骤:1)将设计位图灰度化;2)灰度图像二值化;3)将二值图像去噪,保证轮廓信息的正确性,避免噪音的干扰;4)使用Canny算子将去噪后的图像提取轮廓,得到切割轮廓的所有节点;5)初步剔除掉得到的轮廓中不需要进行切割的轮廓,并将确定为闭合轮廓的非闭合轮廓拼接起来;6)剔除掉轮廓中处在同一条直线上的冗余节点,在不影响切割效果的情况下提高了切割速度,重复步骤6),直至剔除掉所有的冗余节点;7)去除掉内轮廓中包含的轮廓,去除掉得到的所有轮廓中不需要切割的轮廓。本发明在极大
