基于数控加工路径最小化修正的轮廓误差预补偿方法.pdf

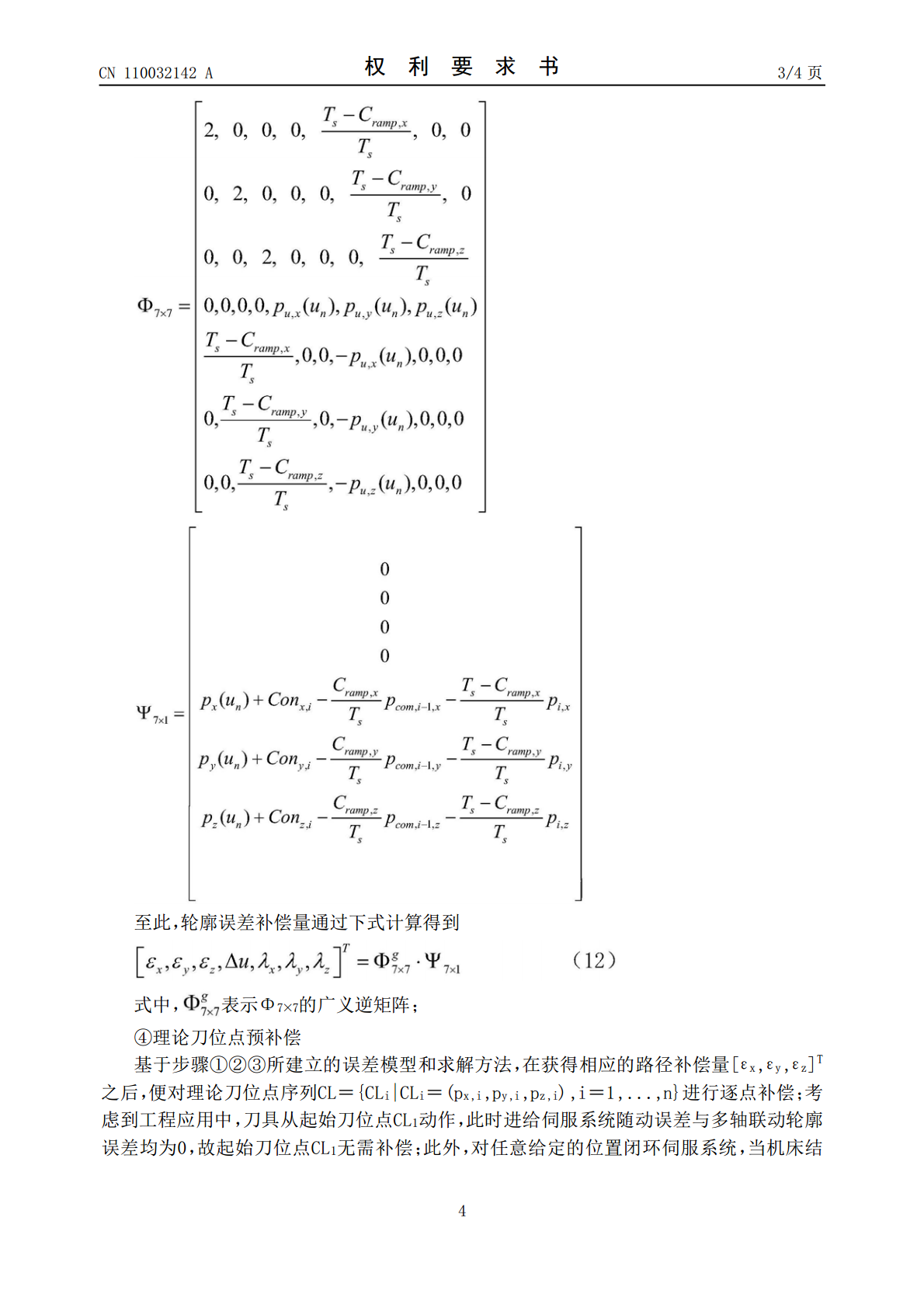
(19)中华人民共和国国家知识产权局(12)发明专利申请(10)申请公布号CN110032142A(43)申请公布日2019.07.19(21)申请号201910354964.9(22)申请日2019.04.29(71)申请人大连理工大学地址116024辽宁省大连市甘井子区凌工路2号(72)发明人孙玉文陈满森徐金亭(74)专利代理机构大连理工大学专利中心21200代理人温福雪侯明远(51)Int.Cl.G05B19/404(2006.01)权利要求书4页说明书10页附图2页(54)发明名称基于数控加工路径最小化修正的轮廓误差预补偿方法(57)摘要本发明提供基于数控加工路径最小化修正的轮廓误差预补偿方法，属于数控加工领域。首先，基于伺服系统对典型输入信号的误差响应，建立了机床进给系统随动误差与刀位指令序列的时域解析关系，给出了一种递进式随动误差预测模型，用于预估机床实际刀位点；其次，基于泰勒展开式的线性化表达，建立了以刀位点补偿量最小为优化目标、以轮廓误差为零为边界约束条件的二次规划模型，并通过引入拉格朗日乘子，进一步将非线性轮廓误差补偿问题转换为线性方程组求解问题；最后，采用递进求解方式，通过逐点修正理论刀位点序列，实现轮廓误差的预补偿。与经典的镜像预补偿法相比，本发明具有算法鲁棒性强、补偿精度高的显著特点，应用于任意m，m≤5轴数控加工系统。CN110032142ACN110032142A权利要求书1/4页1.一种基于数控加工路径最小化修正的轮廓误差预补偿方法，其特征在于，步骤如下：假定所期望轮廓轨迹p(u)为k次B样条参数曲线，其中，u为归一化路径参数，且u∈[0,1]，在机床给定的运动规划算法下，生成的理论刀位点序列为CL＝{CLi|CLi＝(px,i,py,i,pz,i),i＝1,...,n}，其序列间隔为插补周期Ts，n表示插补刀位点数目；按如下步骤实现数控加工路径的轮廓误差补偿：①机床各轴的随动误差预测基于比例控制器控制的位置闭环伺服驱动系统在其阻尼比ζ满足0.707<ζ<1条件时，其系统传递函数Gξ(s)表示为其中，Kξ(ξ＝x,y,z)为系统时间常数；已知理论刀位点CLi＝(px,i,py,i,pz,i)和插补周期Ts，则机床各轴的速度表示为其中，理论刀位点CLi＝(px,i,py,i,pz,i)作为斜坡信号以时间间隔Ts连续输送至进给驱动系统，其随动误差表示为其中，Kramp,ξ,j＝vξ,j；进而，利用下述公式计算得到实际刀位点R_CLi的模型预估值②轮廓误差补偿建模假设基于模型预估的实际刀位点R_CLi在期望轮廓轨迹p(u)上所对应的最近点坐标为pT(un)＝(px(un),py(un),pz(un))；经路径补偿后，指令刀位点被调整为C_CLi＝(pcom,i,x,TTTpcom,i,y,pcom,i,z)＝(px,i+εx,py,i+εy,pz,i+εz)，其中，ε＝(εx,εy,εz)为刀位点补偿量；与此同T时，路径调整后，预估的实际刀位点变为RC_CLi＝(rc_px,i,rc_py,i,rc_pz,i)，且RC_CLi在期T望轮廓轨迹p(u)上对应的最近点坐标为p(un+Δu)＝(px(un+Δu),py(un+Δu),pz(un+Δu))；补偿前后，最近点坐标p(un)，p(un+Δu)满足以下关系p(un+Δu)＝p(un)+pu(un)Δu+δ(un)(5)式中，pu(un)表示期望轮廓轨迹p(u)对其路径参数u的一阶微分，δ(un)为p(un+Δu)泰勒展开式的高阶余项；结合公式(3)和(4)，得调整后预估的实际刀位点RC_CLi坐标为2CN110032142A权利要求书2/4页式中，为保证补偿后轮廓误差为零，需使得补偿后预估的实际刀位点RC_CLi落于期望轮廓轨迹p(u)上，结合公式(5)和公式(6)，预估的实际刀位点RC_CLi和最近点坐标p(un+Δu)应满足以下关系RC_CLi＝p(un)+pu(un)Δu+δ(un)(8)忽略泰勒展开式的高阶余项，结合公式(6)，对公式(8)展开得至此，将非线性轮廓误差补偿问题转换为上述欠定方程组求解问题；③轮廓误差补偿量求解以刀位点补偿量即路径补偿量||ε||2最小为优化目标，以补偿后轮廓误差等于零作为边界条件，结合公式(6)和公式(9)，建立如下二次规划模型min:||ε||2s.t.:rc_pξ,i-pξ(un)-pu,ξ(un)Δu＝0(ξ＝x,y,z)之后，利用拉格朗日乘子法，对上述二次规划问题降阶线性化，建立如下能量方程2J＝||ε||+∑ξ＝x,y,zλξ(rc_pξ,i-pξ(un)-pu,ξ(un)Δu)(10)对公式(10)中的可控变量εx,εy,εz,Δu,λx,λy,λz分别求偏导并令其为零，得如下线性方程组TΦ7×7·