第6章常微分方程数值解-豆柴文库

第6章常微分方程数值解.ppt

2024-09-11

10金币

971KB

17页

天马****23

实名认证

内容提供者

1/10

2/10

3/10

4/10

5/10

6/10

7/10

8/10

9/10

10/10

亲，该文档总共17页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

相关资料

第6章常微分方程数值解.ppt

§1欧拉方法/*Euler’sMethod*/欧拉公式的改进：梯形公式/*trapezoidformula*/改进欧拉法/*modifiedEuler’smethod*/§2龙格-库塔法/*Runge-KuttaMethod*/首先希望能确定系数1、2、p，使得到的算法格式有2阶精度，即在的前提假设下，使得Step3:将yi+1与y(xi+1)在xi点的泰勒展开作比较其中i(i=1,…,m)，i(i=2,…,m)和ij(i=2,…,m;j=1,…,i1)均为待定系数，确定这些系数的步骤与

2024-09-11

971KB

常微分方程数值解.ppt

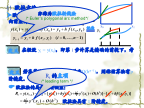
科学研究和工程实践中，有很多实际问题的数学模型都是微分方程。利用微分方程理论，我们可以研究它们的一些性质，对实际问题进行分析。但是，只有极少数特殊的方程有解析解。对于绝大部分的微分方程是没有办法求出它的解析解的。考虑一阶常微分方程的初值问题节点间距hi=xi+1xi为步长，通常采用等距节点，即取hi=h(常数)。一、欧拉(Euler)法与改进欧拉法1.欧拉法：例1用欧拉法求初值问题在区间[0,0.10]上的数值解:n定义欧拉法的局部截断误差：一阶方程的初值问题与积分方程用梯形公式于是有递推格式：Eule

2024-08-30

1.3MB

常微分方程数值解.ppt

§1数值计算方法的意义、内容与方法算法的研究和应用正是本课程的主题！现代科学研究的三大支柱21世纪信息社会的两个主要特征：“计算机无处不在”“数学无处不在”建立数学模型一、计算数学的产生和早期发展数值计算的主要内容§2算法例1：一群小兔一群鸡，两群合到一群里，要数腿共48，要数脑袋整17，多少小兔多少鸡？二、算法的优劣§3误差的背景介绍大家一起猜？据说，美军1910年的一次部队的命令传递是这样的:营长对值班军官:明晚大约8点钟左右，哈雷彗星将可能在这个地区看到，这种彗星每隔76年才能看见一次。命令所有士兵

2024-09-11

1.1MB

常微分方程数值解.ppt

第十章常微分方程数值解考虑一阶常微分方程的初值问题/*Initial-ValueProblem*/:求解(10-1)最基本的方法是单步法由此可见,Euler公式的近似值接近方程的精确值.x0忽略高阶项,取近似值可得到Euler公式隐式欧拉法/*implicitEulermethod*/梯形公式/*trapezoidformula*/注：此法亦称为预测-校正法/*predictor-correctormethod*/。一方面它有较高精度，同时可以看到它是个单步递推格式，比隐式公式的迭代求解过程简单。后面将看

2024-09-17

793KB

数值方法第９章常微分方程数值解（下）.doc

§3单步法的收敛性和绝对稳定性（I）收敛性解出：数值求解微分方程初值问题解，总是要求是的近似，对于Euler方法，我们推导了整体截断误差。满足当时，有，我们注意到这个极限与通常不同。R中点应该是不动的，当，如果用那么这个极限过程当是同时的，而仍固定，这样的极限可以记为并称其为固定态极限（fixedstationlimit）例如：另一种情况定义设初值问题，对y满足Lipschitz条件，如果单步方法（*）得到的解，对任，均有则称单步法是收敛的由收敛性可以推得，对于整体截断误差

2024-08-19

1.2MB