常微分方程数值解.ppt

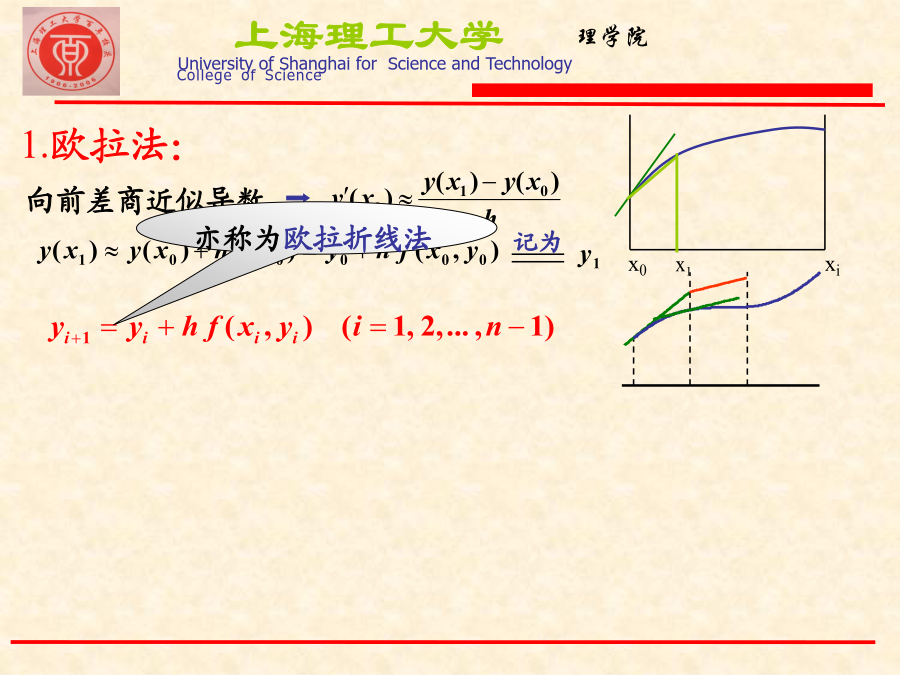
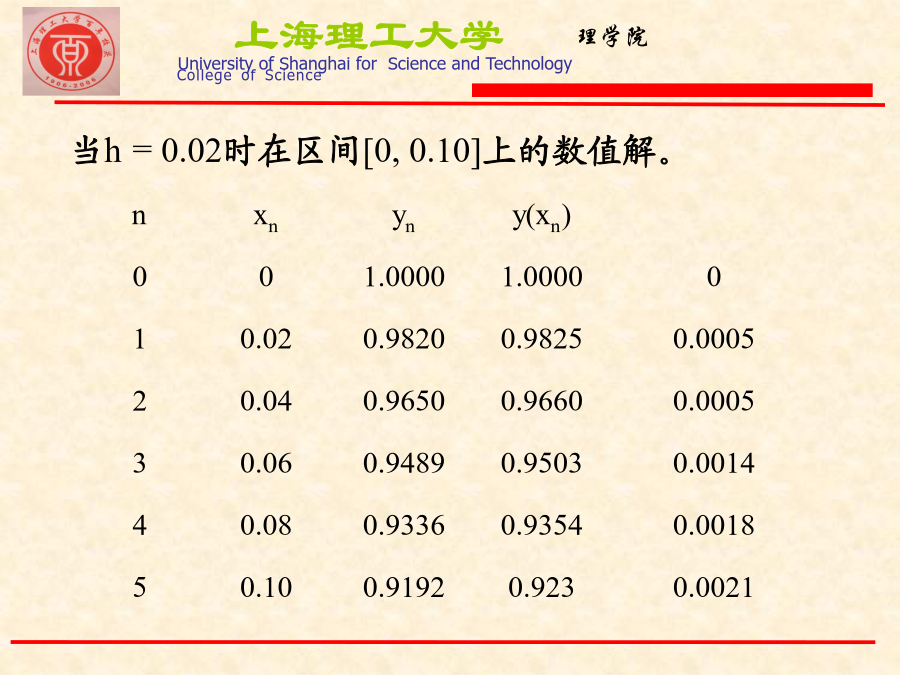
科学研究和工程实践中，有很多实际问题的数学模型都是微分方程。利用微分方程理论，我们可以研究它们的一些性质，对实际问题进行分析。但是，只有极少数特殊的方程有解析解。对于绝大部分的微分方程是没有办法求出它的解析解的。考虑一阶常微分方程的初值问题节点间距hi=xi+1xi为步长，通常采用等距节点，即取hi=h(常数)。一、欧拉(Euler)法与改进欧拉法1.欧拉法：例1用欧拉法求初值问题在区间[0,0.10]上的数值解:n定义欧拉法的局部截断误差：一阶方程的初值问题与积分方程用梯形公式于是有递推格式：Euler公式是求微分方程数值解的很好的方法，它算法简单，易于计算，但Euler方法有一个弱点就是误差较大不能保证精度要求。梯形公式的弱点在于需要解一个方程。改进的Euler公式还有几种不同形式：取步长h=0.1，分别用Euler方法和改进的Euler方法，求微分方程初值问题Euler方法：y0=1,yn+1=yn+hf(xn,yn).xn
3．局部截断误差欧拉法的截断误差：几何解释建立高精度的单步递推格式。首先希望能确定系数1、2、p，使得到的算法格式有2阶精度，即在的前提假设下，使得Step2:将K2代入第1式，得到要求，则必须有：类似的有三阶Runge-Kutta公式：其中i(i=1,…,m)，i(i=2,…,m)和ij(i=2,…,m;j=1,…,i1)均为待定系数，确定这些系数的步骤与前面相似。4阶龙格――库塔法取步长h=0.1，用四阶龙格――库塔法解初值问题xiyiy(xi)(精确解)
0.000000,y0=1.000000y(x0)=1.000000
0.100000,y1=0.905163y(x1)=0.905163
0.200000,y2=0.821269y(x2)=0.821269
0.300000,y3=0.749182y(x3)=0.749182
0.400000,y4=0.689680y(x4)=0.689680
0.500000,y5=0.643470y(x5)=0.643469
0.600000,y6=0.611189y(x6)=0.611188
0.700000,y7=0.593415y(x7)=0.593415
0.800000,y8=0.590672y(x8)=0.590671
0.900000,y9=0.603431y(x9)=0.603430
1.000000,y10=0.632122y(x10)=0.632121写成向量的形式：各种方法都可以直接运用过来。以两个方程的方程组
为例Runge-Kutta公式向量形式Runge-Kutta公式一般形式：例题：求微分方程组x0=0.000000,y0=0.000000z0=1.000000
x1=0.100000,y1=0.205342,yy1=0.210000,z1=1.210175,zz1=1.200009
x2=0.200000,y2=0.422806,yy2=0.440006,z2=1.441955,zz2=1.400139
x3=0.300000,y3=0.654718,yy3=0.690043,z3=1.697616,zz3=1.600716
x4=0.400000,y4=0.903649,yy4=0.960182,z4=1.979671,zz4=1.802304
x5=0.500000,y5=1.172443,yy5=1.250564,z5=2.290899,zz5=2.005729
x6=0.600000,y6=1.464238,yy6=1.561426,z6=2.634373,zz6=2.212097
x7=0.700000,y7=1.782506,yy7=1.893128,z7=3.013488,zz7=2.422813
x8=0.800000,y8=2.131082,yy8=2.246191,z8=3.431996,zz8=2.639604
x9=0.900000,y9=2.514206,yy9=2.621320,z9=3.894045,zz9=2.864540
x10=1.000,y10=2.936564,yy10=3.019451,z10=4.404220,zz10=3.100055
1、高阶方程则有：用若干节点处的y及y值的线性组合来近似y(xn+1)。其通式可写为：（1）求出开头几个点上的近似值，即计算“表头”；基于数值积分的构造法例：建立p=1,q=2的显格式例：建立p=2,q=2的隐格式它的截断误差较显格式小，通常也具有更好的稳定性。1.阿当姆斯外推公式对于一般的差分方程由初始误差产生了差分解的误差，实际上是同一差分方程，取不同初值所得到的2组差分解之间的差。这个差不仅于差分方程本身有关，而且与微分