
主成分分析方法.ppt

天马****23









亲,该文档总共33页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

主成分分析方法在主成分分析方法中的应用.docx
主成分分析与因子分析及SPSS实现(一):原理与方法(2014-09-0813:33:57)转载▼一、主成分分析(1)问题提出在问题研究中,为了不遗漏和准确起见,往往会面面俱到,取得大量的指标来进行分析。比如为了研究某种疾病的影响因素,我们可能会收集患者的人口学资料、病史、体征、化验检查等等数十项指标。如果将这些指标直接纳入多元统计分析,不仅会使模型变得复杂不稳定,而且还有可能因为变量之间的多重共线性引起较大的误差。有没有一种办法能对信息进行浓缩,减少变量的个数,同时消除多重共线性?这时,主成分分析隆重登

《主成分分析方法》.ppt
主成分分析方法本节主要内容:在分析多要素的复杂系统中,多变量问题是经常会遇到的。变量太多,无疑会增加分析问题的难度与复杂性,而且在许多实际问题中,多个变量之间是具有一定的相关关系的。因此,人们会很自然地想到,能否在相关分析的基础上,用较少的新变量代替原来较多的旧变量,而且使这些较少的新变量尽可能多地保留原来变量所反映的信息?事实上,这种想法是可以实现的,主成分分析方法就是综合处理这种问题的一种强有力的工具。主成分分析是把原来多个变量划为少数几个综合指标的一种统计分析方法。从数学角度来看,这是一种降维处理技

主成分分析方法.ppt
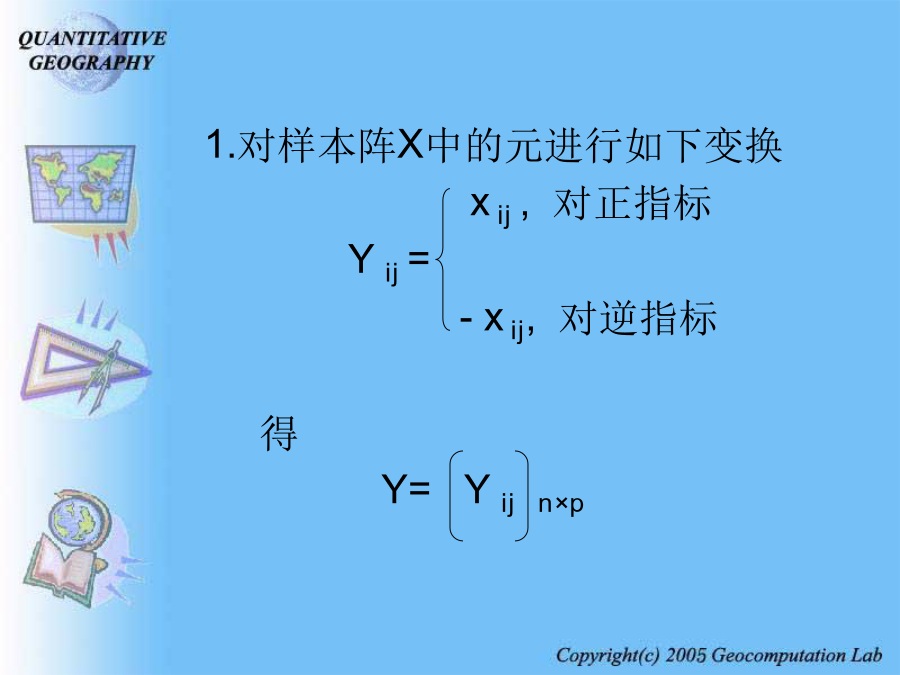
§3.5主成分分析方法基本原理z1,z2,…,zm分别称为原变量指标x1,x2,…,xP的第一,第二,…,第m主成分。主成分分析的主要任务就是确定每一个主成分Zi在原变量xj上的载荷lij系数lij的确定原则:①zi与zj(i≠j;i,j=1,2,…,m)相互无关;②z1是x1,x2,…,xP的一切线性组合中方差最大者,z2是与z1不相关的x1,x2,…,xP的所有线性组合中方差最大者;……;zm是与z1,z2,……,zm-1都不相关的x1,x2,…,xP的所有线性组合中方差最大者。计算步骤3.主成分分析

主成分分析方法.ppt
主成分分析(PrincipalComponentsAnalysis)是由Hotelling于1933年首先提出的,它是利用降维的思想,把多指标转化为少数几个综合指标的多元统计分析方法。从数学角度来看,这是一种降维处理技术。主成分分析的目的与功能主成分的主要功能一、主成分分析的基本原理当m较大时,在m维空间中考察问题比较麻烦。为了克服这一困难,就需要进行降维处理,即用较少的几个综合指标代替原来较多的变量指标,而且使这些较少的综合指标既能尽量多地反映原来较多变量指标所反映的信息,同时它们之间又是彼此独立的。定

主成分分析方法综述.docx
主成分分析方法综述主成分分析(PCA)是一种数据分析方法,它被广泛应用于各种领域,包括数据挖掘、机器学习、图像处理和生物统计学等。PCA是一种线性变换方法,它可以将原始数据集转换为一组新的无关变量,这些新变量被称为主成分。本文将综述PCA的原理、应用和优点。一、PCA的原理PCA的基本思想是将数据集投影到一个新的坐标系中,使得在新的坐标系中能够最大程度上保留原始数据集中的方差。这个新的坐标系由一组与原始数据集的各个维度无关的主成分构成,每个主成分都是原始数据集中的线性组合。这意味着,主成分是一种按重要性排
