
状态空间模型和卡尔曼滤波.ppt

天马****23







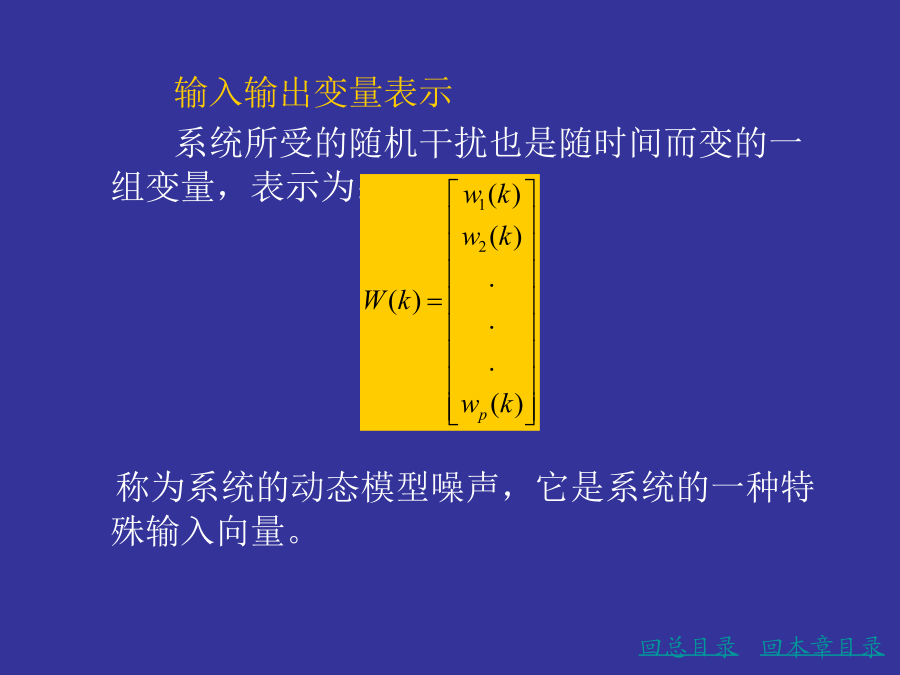
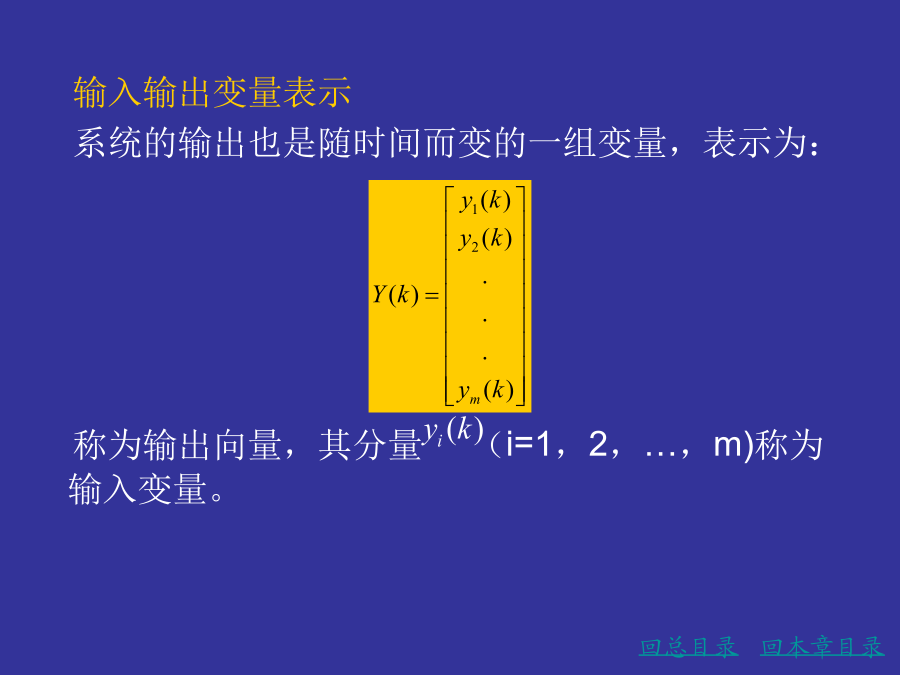

亲,该文档总共19页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

状态空间模型和卡尔曼滤波.ppt
11.1状态空间模型状态空间模型分类状态空间模型按所受影响因素的不同分为:(1)确定性状态空间模型(2)随机性状态空间模型状态空间模型按数值形式分为:(1)离散空间状态模型(2)连续空间状态模型状态空间模型按所描述的动态系统可以分为:(1)线性的与非线性的(2)时变的与时不变的二、系统的状态空间离散事件随机性系统的概念是系统理论中最基本的概念。离散事件随机性系统的状态,是指系统内部的可能运动状态和可能储能状态。系统在k=k0时刻的状态,是在k<k0时以系统内部储能的积累结果,并在k=k0时以系统要素储能的

状态空间模型和卡尔曼滤波.ppt
11.1状态空间模型状态空间模型分类状态空间模型按所受影响因素的不同分为:(1)确定性状态空间模型(2)随机性状态空间模型状态空间模型按数值形式分为:(1)离散空间状态模型(2)连续空间状态模型状态空间模型按所描述的动态系统可以分为:(1)线性的与非线性的(2)时变的与时不变的二、系统的状态空间离散事件随机性系统的概念是系统理论中最基本的概念。离散事件随机性系统的状态,是指系统内部的可能运动状态和可能储能状态。系统在k=k0时刻的状态,是在k<k0时以系统内部储能的积累结果,并在k=k0时以系统要素储能的

状态空间模型和卡尔曼滤波.ppt
第11章状态空间模型和卡尔曼滤波在一般的统计模型中出现的变量都是可以观测到的,这些模型以反映过去经济变动的时间序列数据为基础,利用回归或时间序列分析等方法估计参数,进而预测未来的值。状态空间模型的特点是提出了“状态”这一概念。实际上,无论是工程控制问题中出现的某些状态(如导弹轨迹)还是经济系统所存在的某些状态都是一种不可观测的变量,正是这种观测不到的变量反映了系统所具有的真实状态,所以被称为状态向量。这种含有不可观测变量的模型被称为UC模型(UnobservableComponentModel),UC模型

第状态空间模型和卡尔曼滤波.pptx
会计学23456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108

第状态空间模型和卡尔曼滤波学习教案.pptx
会计学23456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108
