
财务管理ppt第二章货币时间价值.ppt

qw****27







亲,该文档总共23页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

财务管理ppt第二章货币时间价值.ppt
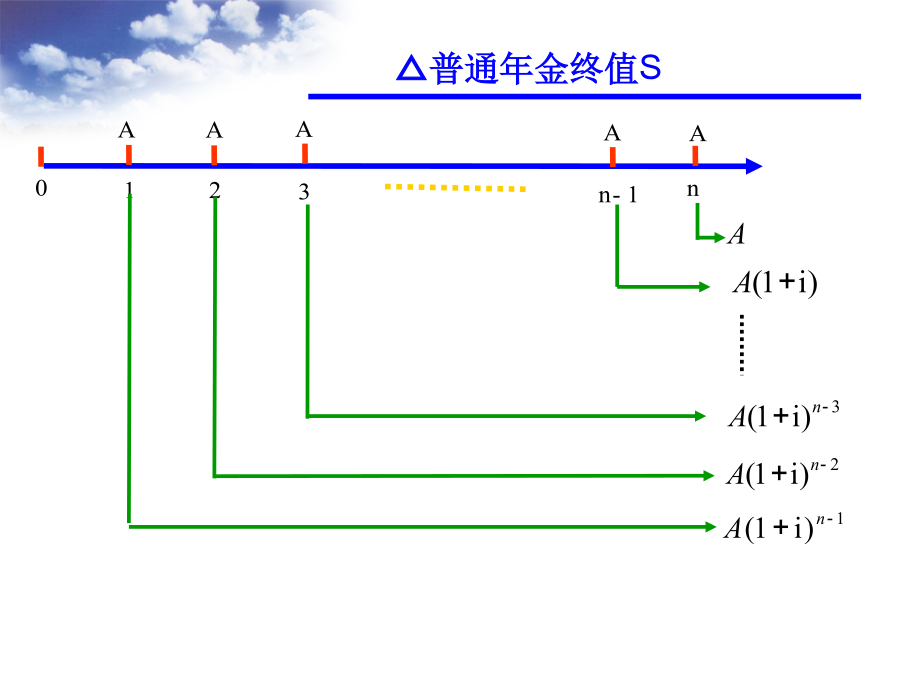
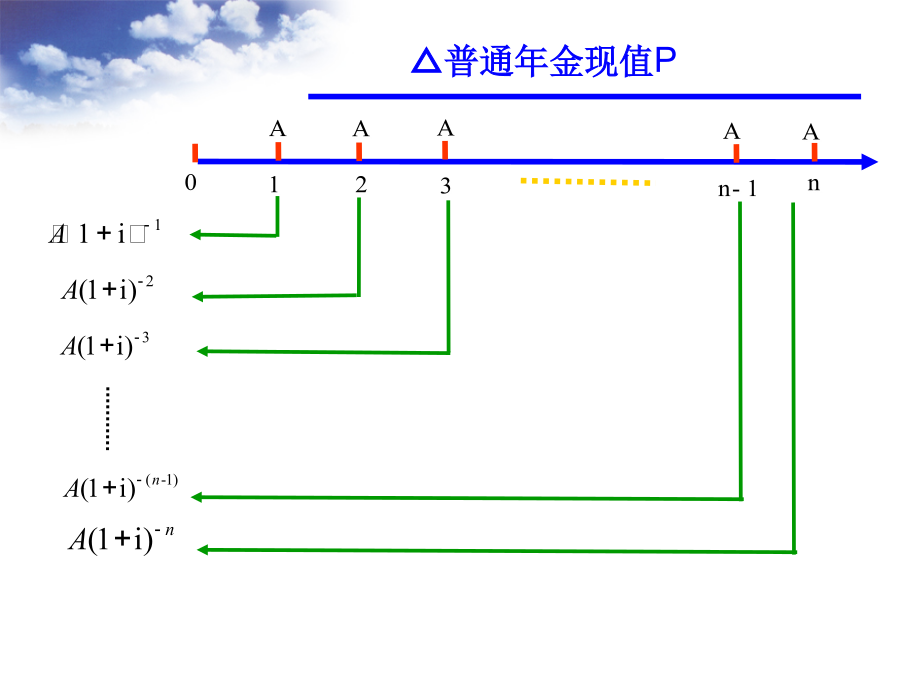
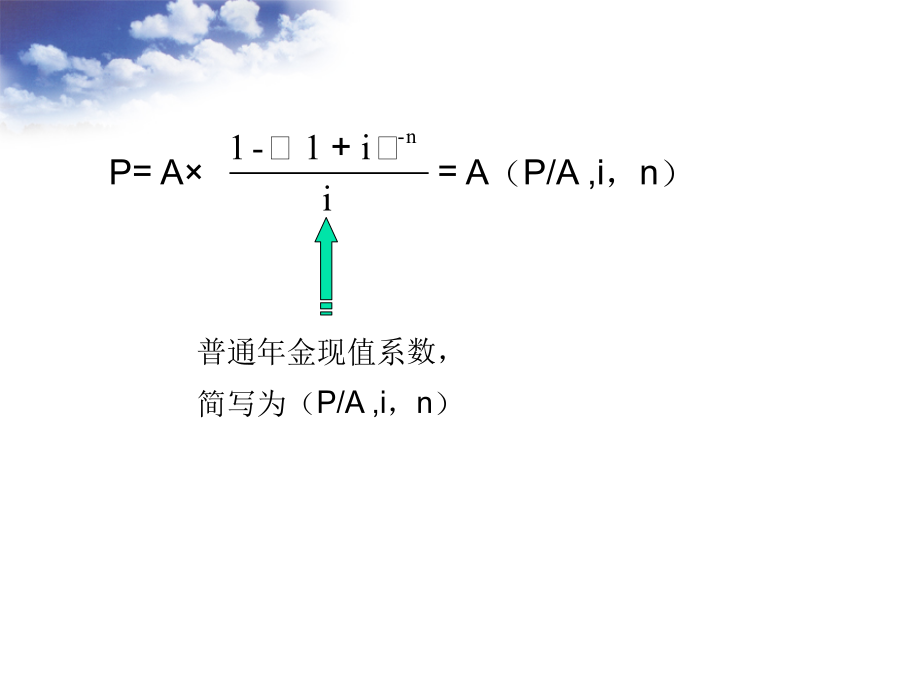
第二章(三)货币时间价值的计算1、单利终值和单利现值3、年金终值和年金现值的计算(1)年金的概念在一定时期内,系列的相等金额的收付款项(收款或付款)。用符号“A”表示。(2)年金的种类A、按年金收付款时间不同①后付年金:如果每期期末都有相等金额的系列性收付款项,叫后付年金。②先付年金:如果每期期初都有相等金额的系列性收付款项,叫先付年金。B、按收付款的特点不同①递延年金:第一次收付款发生在第二期或第二期以后的年金。②永续年金:无限期的等额收付款项。又叫终身年金。n-1S=A×=A(S/A,i,n)n-1P

财务管理第二章货币时间价值PPT课件.ppt
第二章(三)货币时间价值的计算1、单利终值和单利现值3、年金终值和年金现值的计算(1)年金的概念在一定时期内,系列的相等金额的收付款项(收款或付款)。用符号“A”表示。(2)年金的种类A、按年金收付款时间不同①后付年金:如果每期期末都有相等金额的系列性收付款项,叫后付年金。②先付年金:如果每期期初都有相等金额的系列性收付款项,叫先付年金。B、按收付款的特点不同①递延年金:第一次收付款发生在第二期或第二期以后的年金。②永续年金:无限期的等额收付款项。又叫终身年金。n-1S=A×=A(S/A,i,n)n-1P

财务管理ppt-货币时间价值ppt.ppt
货币时间价值课前思考:选择题一、货币时间价值的概念资金时间价值的概念:货币经历一定时间的投资和再投资所增加的价值,也称为货币时间价值。二、资金时间价值表示方式第二节资金时间价值的计算终值(F):现在一定量资金在未来某一时点上的价值。(一)单利某人有资金10000元,拟存入银行,年利率为10%,单利计算,求三年后的终值及利息。答案:终值为13000元,利息为3000元。(二)复利当n=1时:F1=p×(1+i)=10000×(1+6%)=10600元复利终值系数表2、复利现值(p)复利现值系数(二)年金(A

财务管理-货币时间价值PPT课件.ppt
第3章货币时间价值关键概念和技巧引例11终值和复利计算5复利终值计算公式:F=P×(1+r)n式中P—期初投资金额(本金)r—利息率n—投资所持续时的期数或记作(F/P,r,n)2.现值和贴现2.现值的计算和贴现例1:10根据现值、终值、期数求利率?假设一所大学的教育费用在你的孩子18岁上大学时总数将达到$50,000。你今天有$5,000用于投资。利息率为多少时你从投资中获得的收入可以解决你孩子的教育费用?解r:FVT=PV(1+r)T50000=5000x(1+r)18(1+r)18=10(1+r)=

财务管理第二章 货币时间价值.ppt
第二章财务管理基础第二章财务管理基础货币时间价值的概念货币时间价值的计算风险与报酬的衡量第一节货币时间价值第二节风险与收益第三节价值评估第一节货币时间价值一、货币的时间价值2.货币时间价值的表现形式货币时间价值的表现形式有两种:3.货币时间价值的确定从绝对量上看货币时间价值是使用货币的机会成本;从相对量上看货币时间价值是指不考虑通货膨胀和风险情况下的社会平均资金利润率。二、货币时间价值的计算二、货币时间价值的计算二货币时间价值的计算(二)计算
