内容提供者
第九章-柱坐标系和球坐标系下的计算法优秀文档.ppt
2024-09-10
10金币
431KB
26页
天马****23
实名认证
内容提供者
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
亲，该文档总共26页，到这已经超出免费预览范围，如果喜欢就直接下载吧～
相关资料
第九章-柱坐标系和球坐标系下的计算法优秀文档.ppt
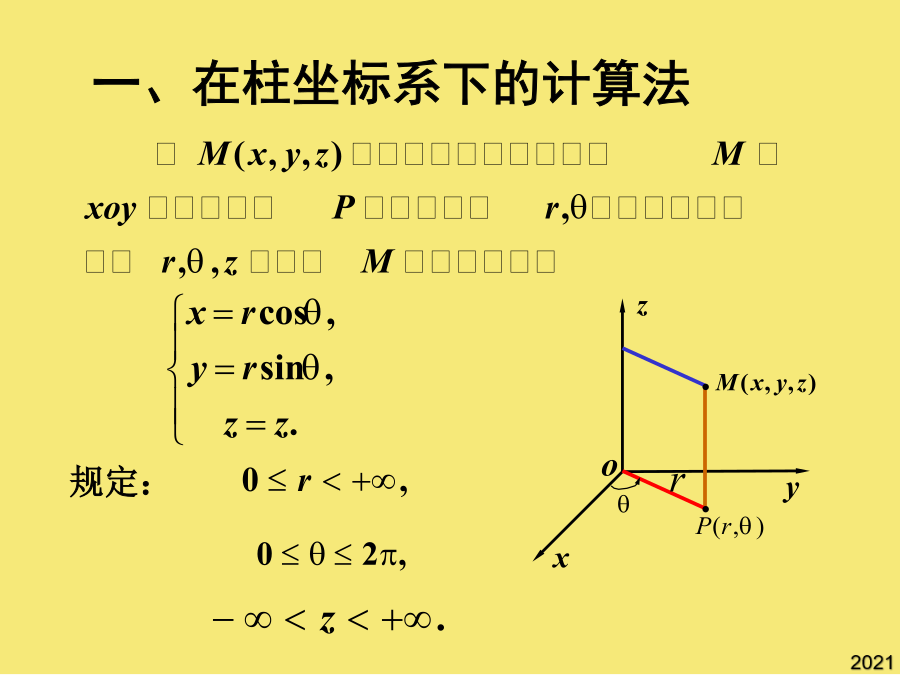
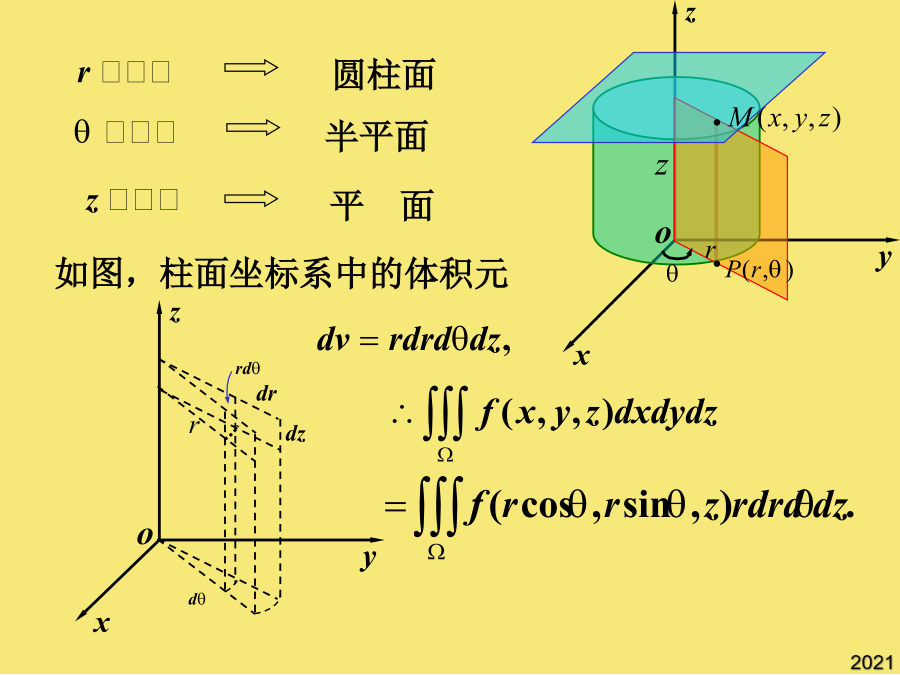
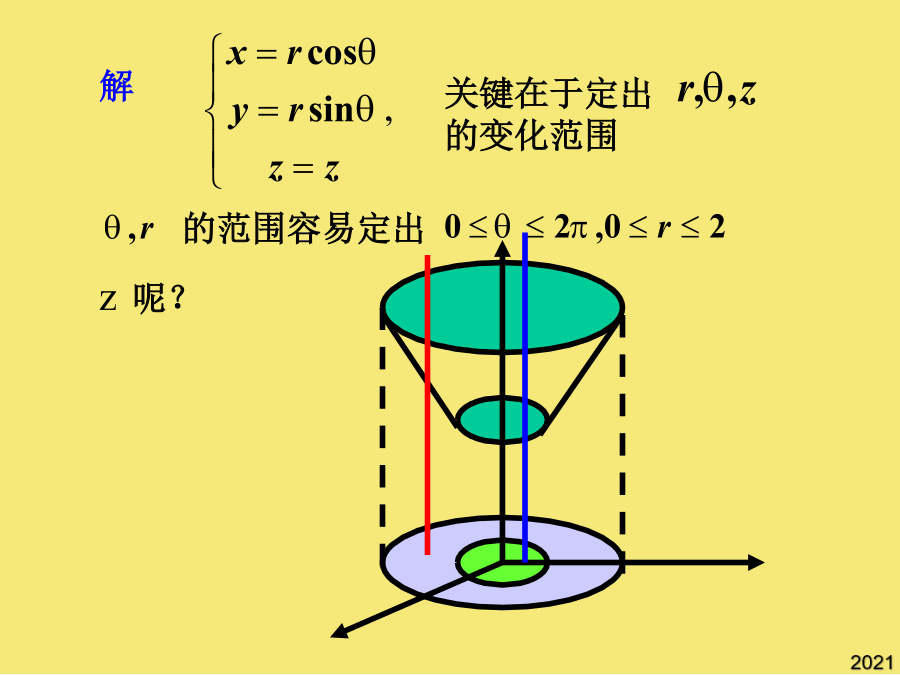
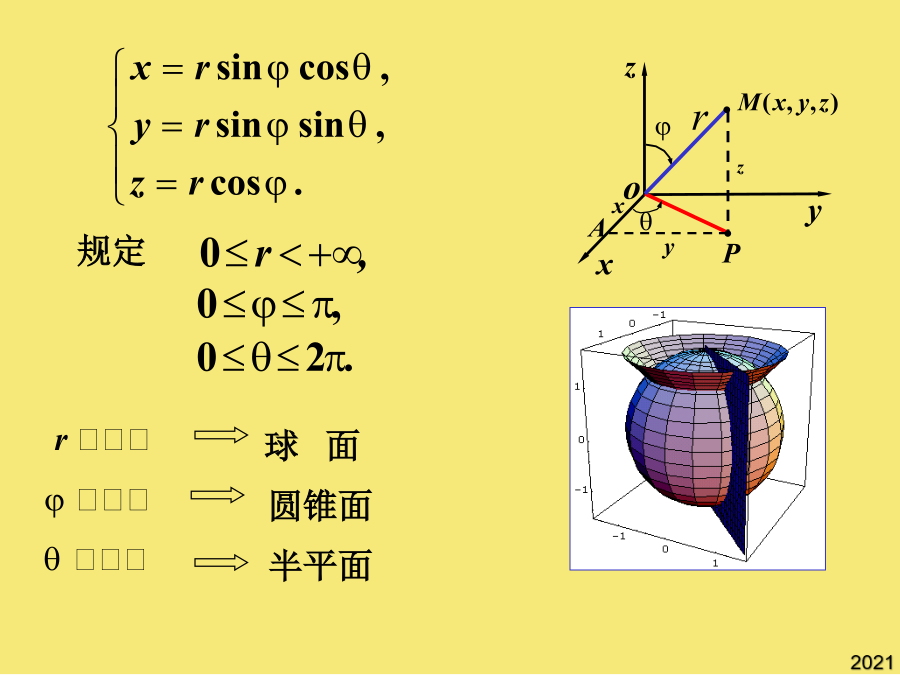
在柱坐标系和球坐标系下的计算一、在柱坐标系下的计算法（1）柱面坐标的体积元素关键在于定出的变化范围若积分区域为球体、球壳或其一部分积分限是根据在积分区域中的变化范围来确定补充：利用对称性简化三重积分计算（1）柱面坐标的体积元素关于xoy面对称１、积分区域关于坐标面的对称性；（1）柱面坐标的体积元素若积分区域为球体、球壳或其一部分补充：利用对称性简化三重积分计算关键在于定出的变化范围积分限是根据在积分区域中的变化范围来确定然后再把它化为三次积分来计算注解注意到二、在球坐标系下的计算法规定如图，球面坐标系中的
2024-09-10
10
431KB
柱坐标系和球坐标系下的计算法.pptx
会计学一、在柱坐标系下的计算法然后再把它化为三次积分来计算注解注意到二、在球坐标系下的计算法如图，球面坐标系中的体积元素为解一解二解注补充：利用对称性简化三重积分计算①③三、小结思考题练习题///练习题答案//
2024-09-15
20
297KB
柱坐标系和球坐标系下的计算法讲义专题培训课件.ppt
柱坐标系和球坐标系下的计算法讲义一、在柱坐标系下的计算法圆柱面然后再把它化为三次积分来计算注解注意到二、在球坐标系下的计算法规定如图，球面坐标系中的体积元素为解一解二解注补充：利用对称性简化三重积分计算①③三、小结思考题练习题练习题答案
2024-11-01
15
411KB
柱坐标系和球坐标系.doc
1.5柱坐标系和球坐标系1.5.1柱坐标系1.5.2球坐标系1.了解柱坐标系、球坐标系的意义，能用柱坐标系、球坐标系刻画简单问题中的点的位置.(重点)2.知道柱坐标、球坐标与空间直角坐标的互化关系与公式.(难点)[基础·初探]1.柱坐标系(1)柱坐标设空间中一点M的直角坐标为(x，y，z)，M点在xOy坐标面上的投影点为M0，M0点在xOy平面上的极坐标为(ρ，θ)，如图151所示，则三个有序数ρ，θ，z构成的数组(ρ，θ，z)称为空间中点M的柱坐标.在柱坐标中，限定ρ≥0,0≤θ<2π，z为任意实数
2024-11-03
10
86KB
柱坐标系和球坐标系.ppt
柱坐标系与球坐标系阅读课本P20---22设P是空间任意一点，柱坐标系又称半极坐标系，它是由平面极坐标系及空间直角坐标系中的一部分建立起来的.试一试试一试二.球坐标系x我们把建立上述对应关系的坐标系叫做球坐标系(或空间极坐标系).空间点P的直角坐标(x,y,z)与球坐标(r,φ,θ)之间的变换关系为试一试数轴
2024-11-02
16
156KB