九随机过程的功率谱密度PPT.ppt

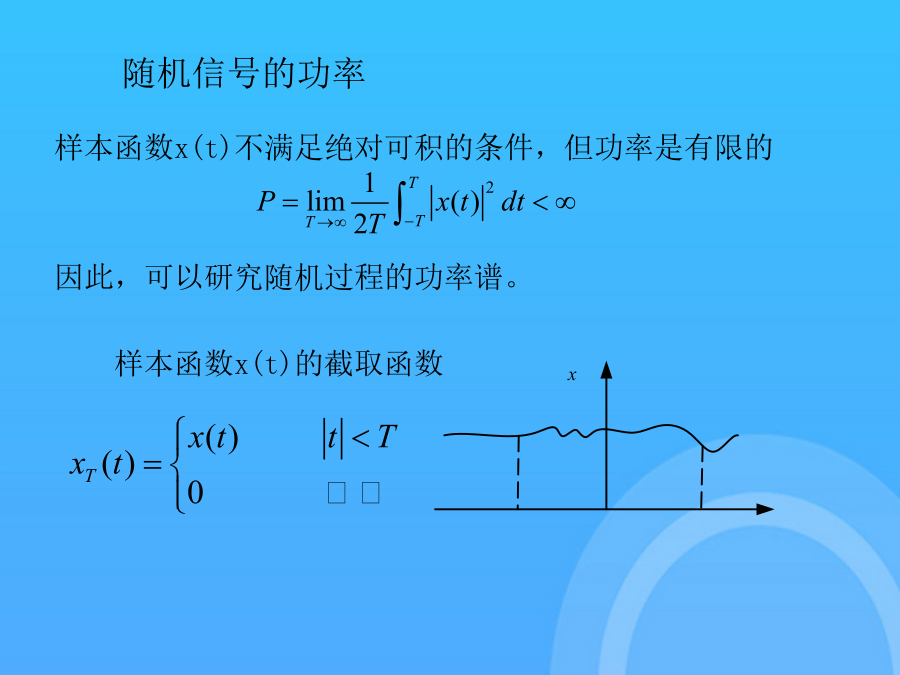
九随机过程的功率谱密度通常用信号在其定义域内的总量来表示信号的大小，称为信号的规范量。
一阶规范量，若模可积，即满足

则一阶规范量定义为

否则定义为
二阶规范量，若模可积定义为

否则定义为

样本函数x(t)不满足绝对可积的条件，但功率是有限的

因此，可以研究随机过程的功率谱。

样本函数x(t)的截取函数
截取函数的傅立叶变换

截取函数应满足帕塞瓦定理

两边同除以2T可得

取集合平均可得

随机过程的平均功率

功率谱密度

两个结论
1、
随机过程的平均功率可以通过对过程的均方值求时间平均得
到。若随机过程广义平稳

2、
若随机过程广义平稳
1、功率谱密度为非负的，即

2、功率谱密度是ω的实函数。
3、对于实随机过程来说，功率谱密度是ω的偶函数，即
截取函数为t的实函数，根据傅立叶变换的性质

于是

4、功率谱密度可积，即
功率谱密度的表达式为

其中

功率谱密度可表示为（3）从功率谱的角度来看：
高斯过程的n维概率密度函数为：
联合平稳随机过程的互谱密度
1、功率谱密度为非负的，即
如果N(t)的功率谱密度集中在为中心的
若平稳过程N(t)在有限频带上的功率谱密度为常
（2）根据噪声的分布：
二者满足绝对可积的条件，则
1、功率谱密度为非负的，即
下面求平均功率
的平稳过程N(t)，称为白噪声过程，简称为
性质5：若正态随机过程在T上是均方可微
性质5：若正态随机过程在T上是均方可微
二者满足绝对可积的条件，则
C为协方差矩阵

对于广义平稳随机过程

则

维纳－辛钦定理样本函数x(t)的截取函数
1、功率谱密度为非负的，即
功率谱密度与自相关函数
随机过程的平均功率可以通过对过程的均方值求时间平均得
二阶规范量，若模可积定义为
性质1：宽平稳高斯过程一定是严平稳过程。
样本函数x(t)的截取函数
2、功率谱密度是ω的实函数。
若平稳过程N(t)在有限频带上的功率谱密度为常
性质3：平稳高斯过程与确定时间信号之和
下面求平均功率
色噪声：功率谱中各种频率分量的大小不同。
功率谱密度与自相关函数
二者满足绝对可积的条件，则
高斯过程定义：如果对于任意时刻，随机过程的任意n维随机变量服从高斯分布，则X(t)就是高斯过程。
自相关函数为互谱密度
定义两个截取函数为

二者满足绝对可积的条件，则
定义两随机过程的互功率为

应用帕塞瓦定理下面求平均功率

，得平均功率

互功率谱密度定义为
1、对于实随机过程X(t)、Y(t)有

2、若X(t),Y(t)联合平稳，有
高斯过程定义：如果对于任意时刻，随机过程的任意n维随机变量服从高斯分布，则X(t)就是高斯过程。高斯过程的n维概率密度函数为：

式中m,x为n维向量

C为协方差矩阵广义平稳正态过程定义：若正态随机过程X(t)的均值和方差都是与时间无关的常数，而自相关函数只取决于时间间隔，则称此正态过程为广义平稳正态过程。性质1：宽平稳高斯过程一定是严平稳过程。
性质2：若平稳高斯过程在任意两个不同时
刻是不相关的，那么也一定是互相独立的
性质3：平稳高斯过程与确定时间信号之和
仍是高斯过程。
性质4：若正态随机过程在T上是均方可
积的，则

也是正态过程。
性质5：若正态随机过程在T上是均方可微
的，则其导数也是正态过程。（1）从噪声与电子系统的关系来看：
内部噪声：系统本身的元器件及电路产生的。
外部噪声：包括电子系统之外的所有噪声。
（2）根据噪声的分布：
高斯噪声：具有高斯分布的噪声。
均匀噪声：具有均匀分布的噪声。
（3）从功率谱的角度来看：
白噪声：如果一个随机过程的功率谱为常数，无论是什么分布，都称它为白噪声。
色噪声：功率谱中各种频率分量的大小不同。一个均值为零，功率谱密度在整个频率轴
上为非零常数，即

的平稳过程N(t)，称为白噪声过程，简称为
白噪声。
利用傅立叶反变换可求得白噪声的自相关函数为：

白噪声的相关系数

若平稳过程N(t)在有限频带上的功率谱密度为常
数，在频带之外为零，则称N(t)为理想带限白噪声。若白噪声的功率谱在内不为零，而在其外为零，
且分布均匀，其表达式为

称这类白噪声为低通白噪声。
自相关函数为如果N(t)的功率谱密度集中在为中心的
频带内，则称N(t)是带通限带白噪声，或称
为带通白噪声，其功率谱为

自相关函数为谢谢观看！感谢观看