复变函数与积分变换.ppt

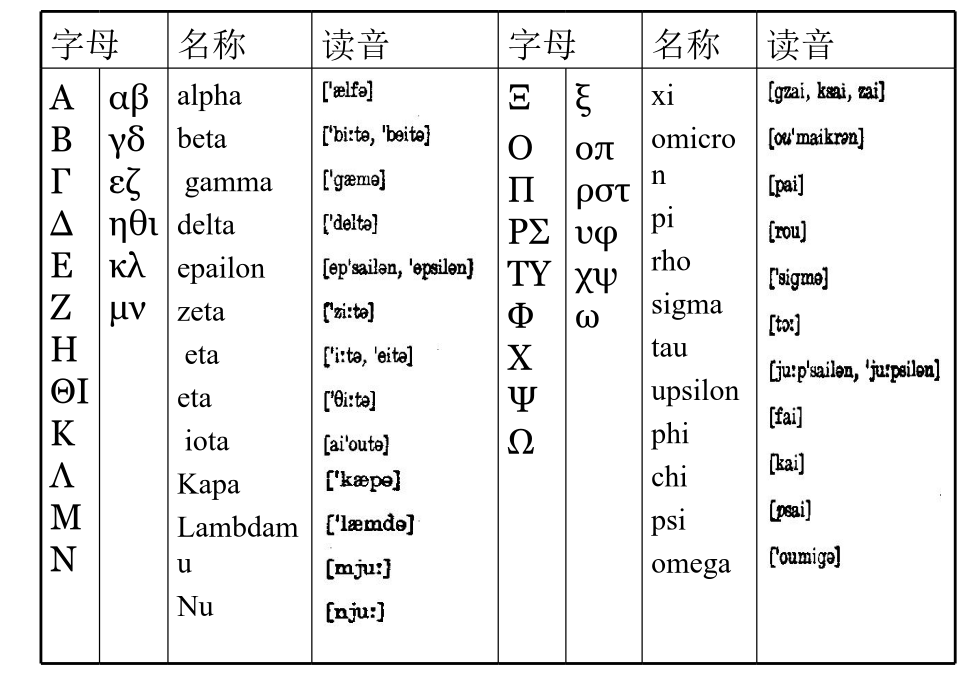
知识、技术

科学知识、技术

专业知识、技术数学物理方法目的、意义：在数学、自然科学、工程技术中有广泛应用。是解决电磁学、信号处理、流体力学、热学等领域中的平面问题的有力工具。
方法：对于复变函数，可类比实函数中的相应概念并稍加区别地理解和掌握。对于数学物理方程部分，结合分离变量与微分方程解法进行学习、理解和掌握。辅以适当的作业练习。
字母第一篇复变函数与积分变换1.1复数及其运算
一：概念
复数z=x+iy,即复数总由实数和纯虚数构成，前为实部，后为虚部，分别称为Rez,Imz,Rez=x,Imz=y
复数与平面点一一对应，该平面是复平面；两坐标轴为实轴，虚轴，若X，Y作为矢分量，则Z可用矢量表示。

复数的表示：
复数形式:代数式z=x+iy（x=cos,y=sin)
极坐标.三角形式：Z=(cos+isin),=(x2+y2)1/2,=arctg(y／x)
指数形式：z=ei，(欧拉公式：ei=cos+isin)
为模，辐角，=Arg(z).二、复球面
无限远点:将球的南极与复平面的原点重合，则北极与复平面上的点的连线交于球面上的一点，故可用球面上的这点描述复平面上的点，或者说复平面上的点与球面上的点一一对应，球面称为复球面，复平面上的无穷远点与北极相对应，记作∞三、复数运算
和，差，积，商，开方运算：不同运算采用不同的复数形式，可简化运算。
A:和,差,运算宜采用代数形式。
B:积,商,开方宜采用三角指数形式。
棣模弗公式：Zn=[reiθ]n=rneinθ=rn(cos(nθ)+isin(nθ))
注意：一般不作声明，是对主值进行运算。
此外：可借用矢量的运算法则，加减用三角形法则，乘用矢量的伸缩旋转。
共轭运算：

取模运算：例：
(1+cos+isin)3=(2cos2(/2)+i2sin(/2)cos(/2))3
=[(2cos(/2)(cos(/2)+isin(/2))]3
=(2cos(/2))3(cos(3/2)+isin(3/2))1.2复变函数复三角函数的模可能大于1,例:|cosi|=(e-1+e)/2﹥1
|sin2i|=(e2-e-2)/2﹥1
将复变函数f(z)的实部.虚部分别记为u(x,y),v(x,y)则f(z)=u(x,y)+iv(x,y)可见一对二元实函数相对应，故实函数性质可移植到复变函数中四、复变函数的极限与连续性1.3导数及C-R条件二、柯西--黎曼条件（C—R条件）一概念：
若函数f(z)在点z0及其邻域上处处可导,则函数在z0处解析。
若函数f(z)在区域B上每点都解析,则称f(z)在区域B上解析.
若函数f(z)在z0点不解析,则点z0是f(z)的奇点.2:若f(z)=u+iv在B上解析则u,v均为B上的调和函数（有连续二阶偏导数且满足拉氏方程▽2u=0）对条件形式，两边分别再求一次导,即通常都采用不定积分发比较可靠例:已知解析函数f(z)=u+iv的u=x3-3xy2,求v及f(z)1.5平面标量场故v(x,y)又叫通量函数。无旋平面液流：稳流时，速度矢量可用一标量的梯度表示即v=▽Φ,此标量Φ为速度势，取解析函数f(z)=u+iv的v为速度势,u(x,y)=常量是流线族，流量Q=uA(x1,y1)-uB(x1,y1)例：平面静电场的电力线为y2=c2+2cx(c>0)的抛物线,求等势线。*1.6多值函数Ch2复变函数的积分2.2柯西定理定理：
若在闭合复连通区域上的单值解析函数,则
L为区域外边界线,Li为区域内边界线.积分均为边界线正向。说明：如图作辅助线，使其变为单连域。2.3柯西公式柯西导数公式
对柯西公式两边求导：

在利用此公式计算此积分时，注意将原被积函数写成该被积分式形式：可将求积分转化为求解析函数的导数。
模数原理:设f(z)在某区域解析:则|f(z)|只能在边界上取极大值。
刘维尔定理:若f(z)在全平面上解析,并且是有界,即|f(z)|≤N,f(z)必为常数。Ch3复数项级数3.2幂级数幂级数在其收敛圆内绝对收敛，并一致收敛：可对幂级数逐项求导逐项积分，幂级数的和在收敛圆内是解析函数。
例：求幂级数的收敛圆：
收敛圆为：|t|<1此数为几何级数：(前n项和)

例：求幂级数∑（-1）kz2k的收敛圆。
此为间出幂级数：3.3泰勒级数展开求f(z)的泰勒级数的方法：
①运用定义定理求②类比实函数的幂级数求出。
③运用级数的运算规律。(加.减.乘.除)
④运用幂级数的复合及逐项求导,积分法。解析延拓3.4洛朗级数展开说明：①展式的展开中心z0可以是奇点，也可以是解析点，如果z0为奇点，圆环区域圆可无限接近z0，在此圆环域的展式为孤立奇点z0邻域展式。②展式系数不能等于fn(z0)/n!

∵